QTKWVCK%VL$R~DMLUGY0~(P.png

梯度下降算法的性质作用

:::info 梯度下降算法是在监督学习中，由模型预测结果与正确结果的差异（损失函数得出的损失值），通过梯度下降的方法对模型内部的算法（可以是线性回归，CNN，等）所含参数（theta等）进行调整，并通过不断重复这种调整最终得到预测准确率较高的模型 :::

对梯度下降算法的理解

注意下图不是函数，函数是J和输入样本X的，J&theta参数图是样本（输入的x）已经输入固定的情况下改变参数theta的大小对J的大小的影响，在梯度下降的过程中实际上得到的是一系列的不连续点。

如图，BP算法中的损失函数J（J的大小表示误差的大小），为了让损失函数J的值减小，我们通过改变J中的参数theta来达到这一目标。
图中是假设J只有theta这一个参数，那么我们把J对theta求导得到J下降的方向（即平行于导数切线，使J下降的方向），在这个方向上，我们规定一个步长n，在导数使J下降的方向上进行每次增大/减小theta大小为
`]W`5_6MBYQ]A8GH]L8H9PY.png
并求得J相应的值。
（原始的theta大多是是随机而来的）
如果把新得到的J再将其对theta进行求导，发现导数仍然不为零，那么就重复上述步骤直到找到最低点位置对应的参数theta大小
]O850J4V0E9O9AM@HFDSG2Q.png

在实际算法中，参数数量非常多，维度非常高，我们利用多元函数微分法，梯度就代表着让J下降最快的所有参数改变的方向，代替导数方向，每次同时改变多个参数大小（同一层的参数皆参与），进行上述步骤。

eta的影响
![QU}C@@@X]$IX~EFT36}O4X.png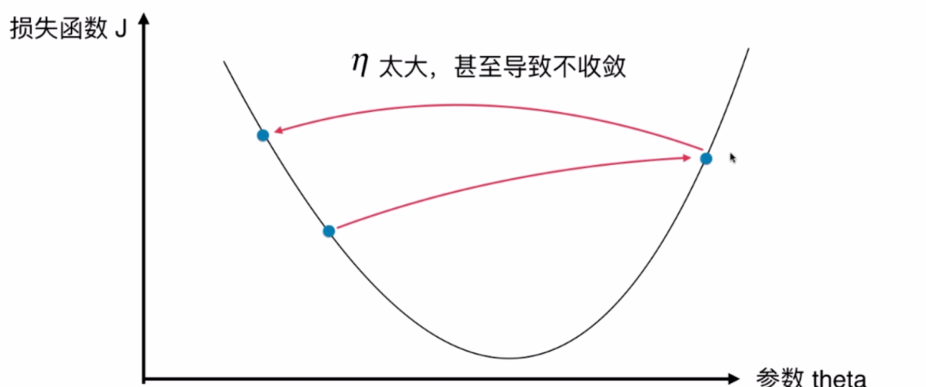~S$)AY4KM%H~$_@1M_Q0~$R.png

:::warning 很多函数都有多个极值点，可能得不到全局最优解 ::: ![JU2`KA%7XH%JTY91ME$HUI.pngEQ~Q55Z7@73TS{BQ}5L3LIN.png

解决方案：多次运行（初始点不同）并比较得到的局部最优解，很有可能通过梯度下降算法得到全局最优解

对梯度下降算法的应用

线性回归中对梯度下降算法的应用![A(6Y(%0QM)HYSK{KS@X4~V.png

![V%61`0[I6ORU93IKK300UF.png

简化之后（累加后除以m使得数据值不大） :::warning 事实上在不同的算法（这里是线性回归）中，损失函数的原生公式各不相同，但是在将原生的损失公式简化的过程中，其目标都是为了得到的损失值比较简洁，合理的减小计算 ::: 0E~C)`Z5FX60U[I_M8_]~]1.png

梯度下降算法的向量化（用矩阵运算简化梯度的计算公式）

`H8X]4W~RD3E~I$N{AE8{%1.png

  1. import numpy as np
  2. from .metrics import r2_score
  4. class LinearRegression:
  6.     def __init__(self):
  7.         """初始化Linear Regression模型"""
  8.         self.coef_ = None
  9.         self.intercept_ = None
  10.         self._theta = None
  11. #普通线性回归算法
  12.     def fit_normal(self, X_train, y_train):
  13.         """根据训练数据集X_train, y_train训练Linear Regression模型"""
  14.         assert X_train.shape[0] == y_train.shape[0], \
  15.             "the size of X_train must be equal to the size of y_train"
  17.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  18.         self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
  20.         self.intercept_ = self._theta[0]
  21.         self.coef_ = self._theta[1:]
  23.         return self
  24. #使用梯度下降法的线性回归算法
  25.     def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
  26.         """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
  27.         assert X_train.shape[0] == y_train.shape[0], \
  28.             "the size of X_train must be equal to the size of y_train"
  30.         def J(theta, X_b, y):
  31.             try:
  32.                 return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
  33.             except:
  34.                 return float('inf')
  36.         def dJ(theta, X_b, y):
  37.             # res = np.empty(len(theta))
  38.             # res[0] = np.sum(X_b.dot(theta) - y)
  39.             # for i in range(1, len(theta)):
  40.             #     res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
  41.             # return res * 2 / len(X_b)
  42. #以下就是对梯度下降算法向量化（矩阵计算）后简化出的式子
  43.             return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(X_b)
  44. #梯度下降法
  45.         def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
  47.             theta = initial_theta
  48.             cur_iter = 0
  50.             while cur_iter < n_iters:
  51.                 gradient = dJ(theta, X_b, y)
  52.                 last_theta = theta
  53.                 theta = theta - eta * gradient
  54.                 if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
  55.                     break
  57.                 cur_iter += 1
  59.             return theta
  61.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  62.         initial_theta = np.zeros(X_b.shape[1])
  63.         self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
  65.         self.intercept_ = self._theta[0]
  66.         self.coef_ = self._theta[1:]
  68.         return self
  69. #使用随机梯度下降法的线性回归算法
  70.     def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
  71.         """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
  72.         assert X_train.shape[0] == y_train.shape[0], \
  73.             "the size of X_train must be equal to the size of y_train"
  74.         assert n_iters >= 1
  76.         def dJ_sgd(theta, X_b_i, y_i):
  77.             return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
  78. #随机梯度下降法
  79.         def sgd(X_b, y, initial_theta, n_iters, t0=5, t1=50):
  81.             def learning_rate(t):
  82.                 return t0 / (t + t1)
  84.             theta = initial_theta
  85.             m = len(X_b)
  87.             for cur_iter in range(n_iters):
  88.                 #乱序索引以保证随机性，而且由乱序从前往后取，保证样本不重复
  89.                 indexes = np.random.permutation(m)
  90.                 X_b_new = X_b[indexes]
  91.                 y_new = y[indexes]
  92.                 #每次遍历仅提取一个特征值来计算不完整梯度
  93.                 for i in range(m):
  94.                     gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
  95.                     theta = theta - learning_rate(cur_iter * m + i) * gradient
  97.             return theta
  99.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  100.         initial_theta = np.random.randn(X_b.shape[1])
  101.         self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
  103.         self.intercept_ = self._theta[0]
  104.         self.coef_ = self._theta[1:]
  106.         return self
  108.     def predict(self, X_predict):
  109.         """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
  110.         assert self.intercept_ is not None and self.coef_ is not None, \
  111.             "must fit before predict!"
  112.         assert X_predict.shape[1] == len(self.coef_), \
  113.             "the feature number of X_predict must be equal to X_train"
  115.         X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
  116.         return X_b.dot(self._theta)
  118.     def score(self, X_test, y_test):
  119.         """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
  121.         y_predict = self.predict(X_test)
  122.         return r2_score(y_test, y_predict)
  124.     def __repr__(self):
  125.         return "LinearRegression()"

随机梯度下降法（SGD）

当样本的特征值过多时，每一次梯度下降都要求得多元函数的梯度（其中包括了对所有特征值分别求偏导），很是消耗算力，这时候我们就要用随机梯度下降进行优化，仅对样本中的一个特征值（例如上面的代码）进行求偏导来计算不完整的梯度来调整参数（一般来说数据集中的一个样本要多次遍历特征值来计算多个不完整梯度），或者也可以对参与训练的样本数目进行调整

随机梯度下降法的优势20220607212756.png
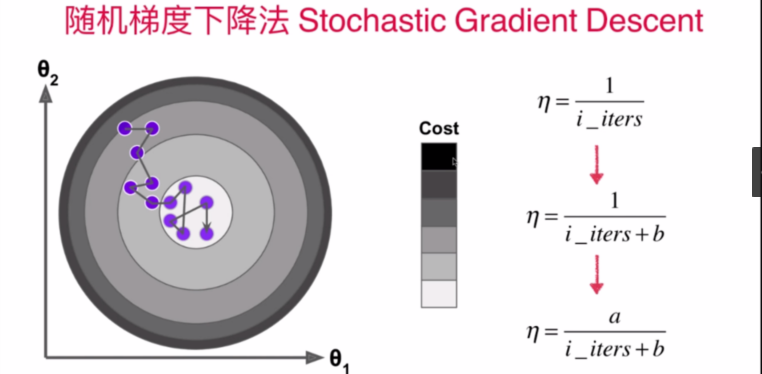
20220607195430.png

这样一来会有一定的不确定性，不过总的说来在一定的随机化范围中是有利的
注意：在随机梯度下降的过程中，可以设置：越接近设定的目标精度，每次下降的步长eta就越小，具体的改变量如上图（加入超参数a，b）

模拟退火的思想： 模拟锻造过程中随着训练消耗的时间的增加而退火（减小步长eta）的方法

@9LGC)J4IQE2MQ`E@KQZ7}H.png

随机梯度下降法中调整n_iter参数的意义

注意在上面的代码块中，n_iter在(批量)梯度下降中代表的是目标精度，而在随机梯度下降中n_iter表示的是所参考的样本倍数（相对于原样本，大于1就随机再重复抽取），m则表示每个样本所抽取的特征值数目

sklearn中的随机梯度下降法封装模块（超级优化模式）

51e9f435-bcc4-4a79-80ec-dee65d4f24ab.png

小批量梯度下降法（灵活，常用，实用性高）

当样本的特征值过多时，每一次梯度下降都要求得多元函数的梯度（其中包括了对所有特征值分别求偏导），很是消耗算力，这时候我们就要用随机梯度下降进行优化，仅对一部分特征值（这里每次取k个特征值，例如下面的代码）进行求偏导来计算不完整的梯度来调整参数（一般来说数据集中的一个样本要多次遍历特征值来计算多个不完整梯度），或者也可以对参与训练的样本数目进行调整

可能存在的问题

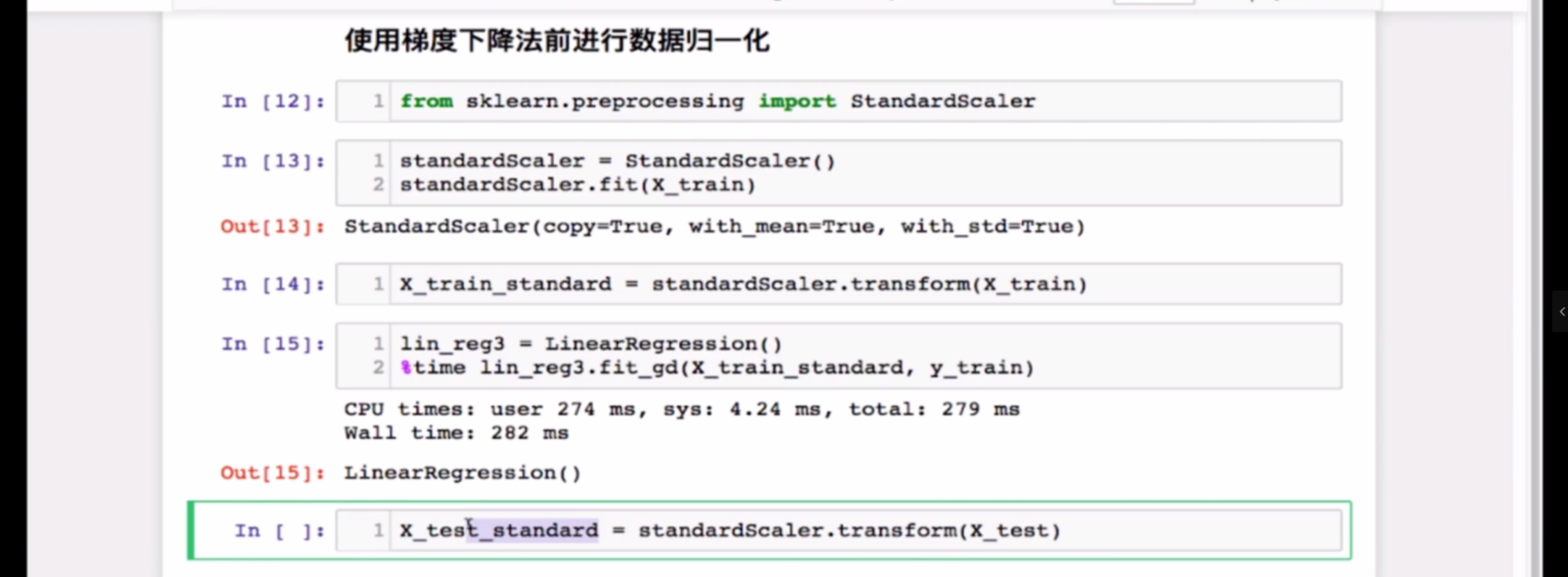
当输入的样本包含多个特征数据，且这些数据之间数值差距过大，可能导致计算出的损失值过大（溢出），值得注意的是，在线性回归算法的损失值计算公式中，需要梯度下降后的y值参与，也就是说有eta参与其中，所以这时可以适当缩小步长eta来减小损失值的数值 但是，eta牵涉的是梯度下降的效率，不宜因为其他原因进行改变 真正合适的解决方法是数据归一化

数据归一化

M_~LD`OQB@WIRKT2XSB_850.png

  1. import numpy as np
  4. class StandardScaler:
  6.     def __init__(self):
  7.         self.mean_ = None
  8.         self.scale_ = None
  10.     def fit(self, X):
  11.         """根据训练数据集X获得数据的均值和方差"""
  12.         assert X.ndim == 2, "The dimension of X must be 2"
  14.         self.mean_ = np.array([np.mean(X[:,i]) for i in range(X.shape[1])])
  15.         self.scale_ = np.array([np.std(X[:,i]) for i in range(X.shape[1])])
  17.         return self
  19.     def transform(self, X):
  20.         """将X根据这个StandardScaler进行均值方差归一化处理"""
  21.         assert X.ndim == 2, "The dimension of X must be 2"
  22.         assert self.mean_ is not None and self.scale_ is not None, \
  23.                "must fit before transform!"
  24.         assert X.shape[1] == len(self.mean_), \
  25.                "the feature number of X must be equal to mean_ and std_"
  27.         resX = np.empty(shape=X.shape, dtype=float)
  28.         for col in range(X.shape[1]):
  29.             resX[:,col] = (X[:,col] - self.mean_[col]) / self.scale_[col]
  30.         return resX

关于梯度的调试

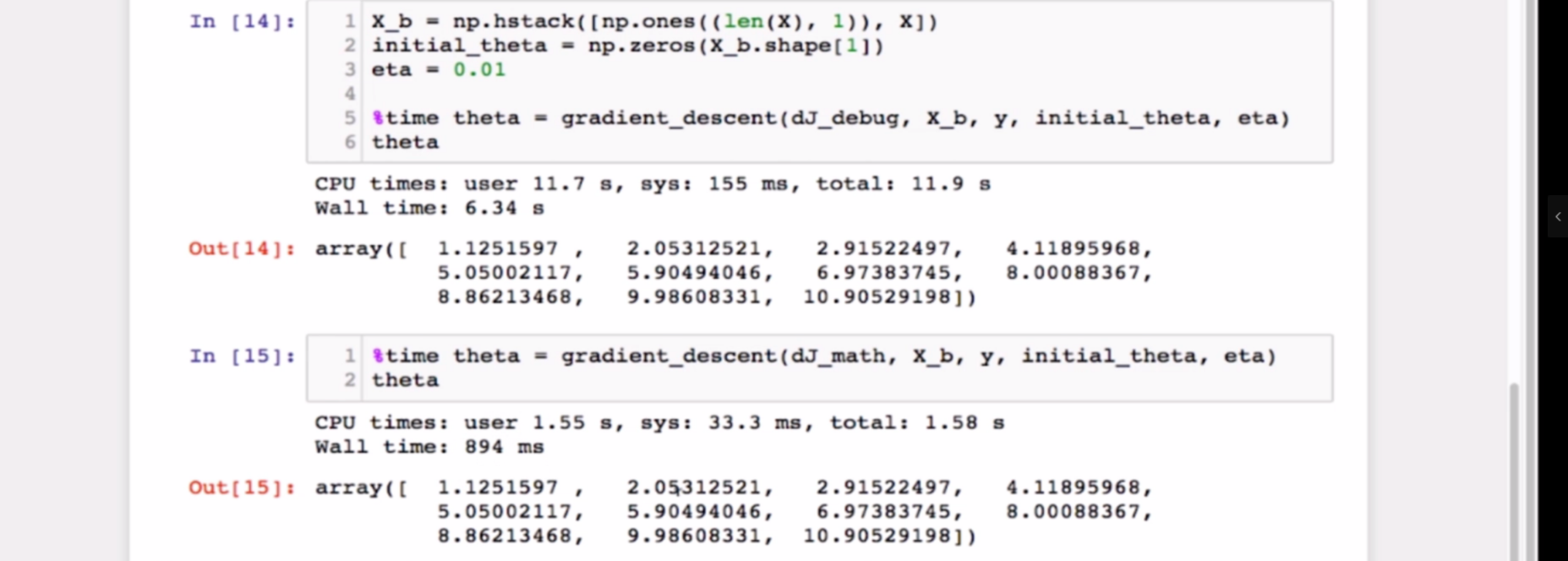
使用贴近于求导点的两点计算近似梯度（导数的定义）来判断求导计算的梯度是否正确

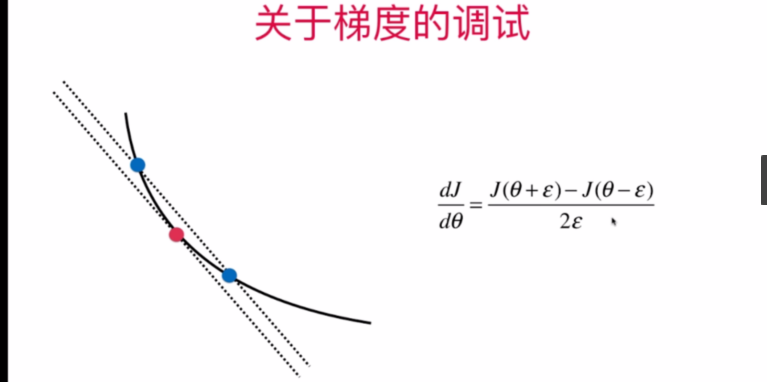
20220607211218.png
多元函数中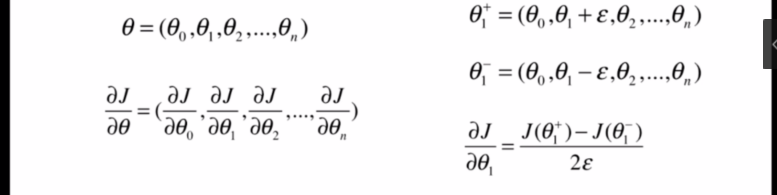
20220607211359.png
代码实现

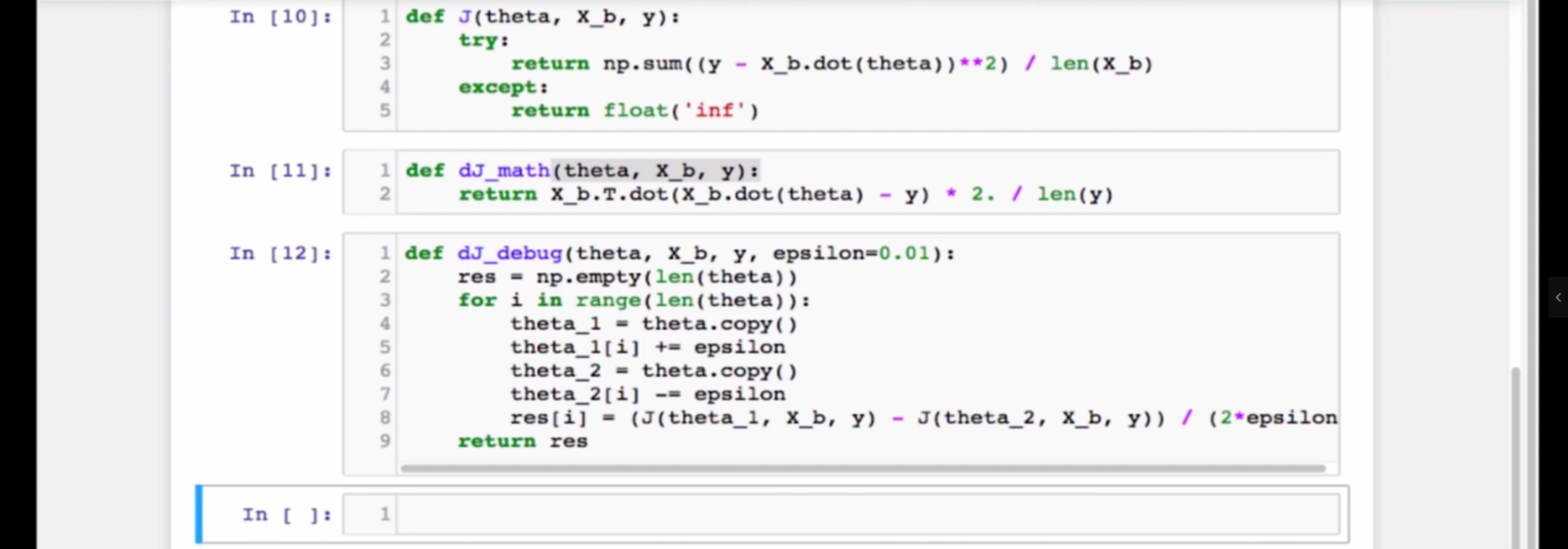
20220607211902.png
值得注意的是，使用极限定义求出来的梯度也可以用于训练，只不过相比数学结论（求导求梯度）计算量更大，只能做测试/小范围用
20220607212119.png

博客参考

(27条消息) 机器学习算法之梯度下降法_mind_programmonkey的博客-CSDN博客.pdf