本章重点

串、数组和广义表 - 图1

串

概述

串的定义：零个或多个任一字符组成的有限序列，又称为字符串(String)。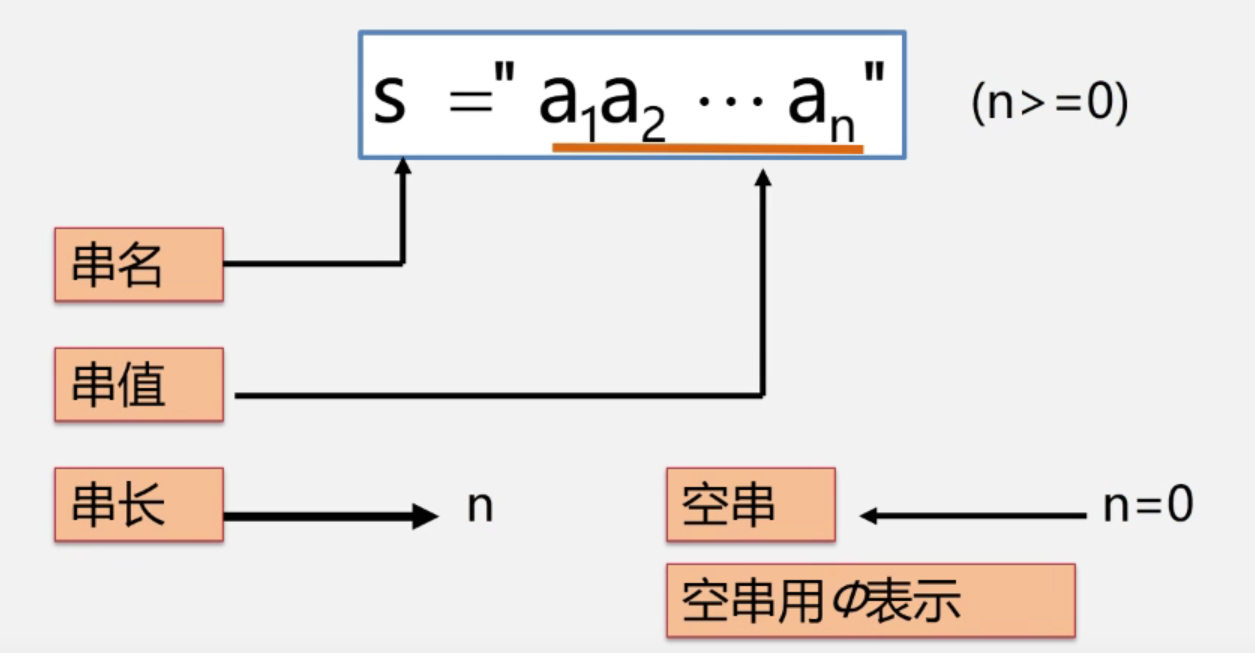
image.png
子串：串中任意个连续字符组成的子序列(含空串)称为该串的子串，真子串是指不包含自身的所有子串。
主串：包含子串的串相应的称为主串。
字符位置：字符在序列中的序号为该字符在串中的位置。
子串位置：子串第一个字符在主串中的位置。
空格串：由一个或多个空格组成的串，与空串不同！

范例：
image.png

串相等：当且仅当两个串的长度相等并且各个对应位置上的字符都相同是，这两个串才相等。所有的空串都是相等的。

案例引入

串的应用非常广泛，计算机上非数值处理的对象大部分都是字符串数据，例如：文本编辑、符号处理、各种信息处理系统等等。

【例】病毒感染检测
研究者将人的DNA和病毒DNA均表示成由一些字母组成的字符串序列，如：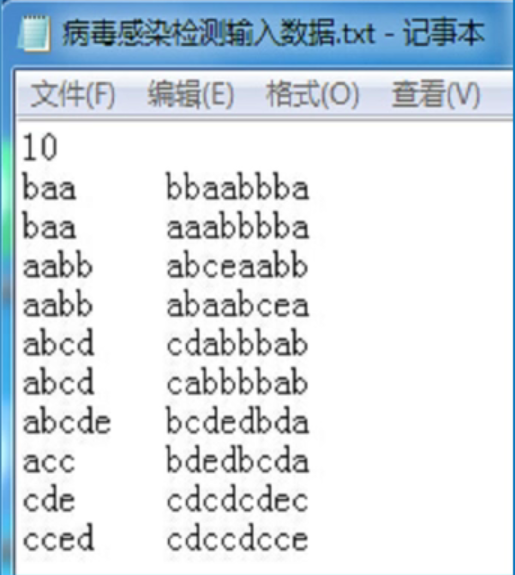
image.png
然后检测某种病毒的DNA序列是否在患者的DNA序列中出现过，如果出现过，则此人感染，否则没有感染。
注意：人的DNA序列是线性的，而病毒的DNA序列是环状的！如图中的两个例子：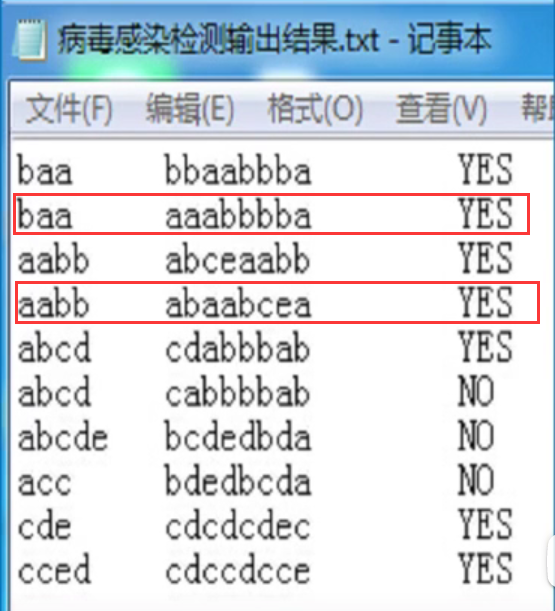
image.png

串的类型定义

image.png
image.png
串和前面的线性表有很多相似的地方，不过这里的数据类型是字符而已。
串中元素逻辑关系与线性表的相同，串可以采用与线性表相同的存储结构，即串也分为顺序串和链串

串的存储结构

串的顺序存储结构

  1. #define MAXLEN 255
  3. typedef struct {
  4.     char ch[MAXLEN + 1];    // 存储串的一维数组
  5.     int length;                // 串的当前长度
  6. } SqString;

串的链式存储结构
image.png
优点：操作方便
缺点：存储密度低
存储密度 = 串值所占的存储空间 / 实际分配的存储空间

为了更加操作方便，所以我们可以把多个字符存放在一个结点中，以克服其缺点
image.png
这种串的链式存储结构，即为块链存储结构

  1.  #define CHUNKSIZE 80    // 块的大小
  3. typedef struct Chunk {
  4.     char ch[CHUNKSIZE];
  5.     struct Chunk* next;
  6. } Chunk;
  8. typedef struct {
  9.     Chunk *head, *tail;        // 串的头指针和尾指针
  10.     int curlen;                // 串的当前长度
  11. } LString;                    // 字符串的块链结构

串的基本操作实现

【Index】确定主串中所含子串(模式串)第一次出现的位置(定位)
算法应用：搜索引擎、拼写检查、语言翻译、数据压缩
算法种类：

  • BF算法，暴力破解
  • KMP算法，速度快，但是比较难理解

BF算法又称简单匹配算法，采用穷举法思路，算法的思路是从S的每一个字符开始依次与T的字符进行匹配
image.png
Index(S,T,pos)

  • 将主串的第pos个字符和模式串的第一个字符比较
    • 若相等，继续逐个比较后续字符；
    • 若不等，从主串的下一字符器，重新与模式串的第一个字符比较
  • 直到主串的第一个连续子串字符序列与模式串相等，返回值为S中与T匹配的子序列的第一个字符的序号，即匹配成功
  • 否则匹配失败，返回0

代码

  1. int Index_BF(SqString* S, SqString* T, int pos) {
  2.     if (pos <= 0) return ERROR;
  3.     int j = 1;
  4.     while (pos <= S->length && j <= T->length) {
  5.         if (S->ch[pos] == T->ch[j]) {
  6.             pos++;
  7.             j++;
  8.         }ababcabcacbab
  9.         else {
  10.             pos = pos - j + 2;
  11.             j = 1;
  12.         }
  13.     }
  15.     return j >= T->length ? pos - T->length : 0;
  16. }

KMP算法

由于BP算法每次 j 匹配不成功都要回溯到1，所以导致算法的效率极低。
由此就有了KMP算法，KMP算法时利用已经部分匹配的结果而加快模式串的滑动速度，且主串S的指针i不必回溯，时间复杂度可以提升至O(n+m)。
此算法的是这样的，假设我们有主串S = “ababcabcacbab” 和 子串T = “abcac”，当我们进行第一次比较时，如图：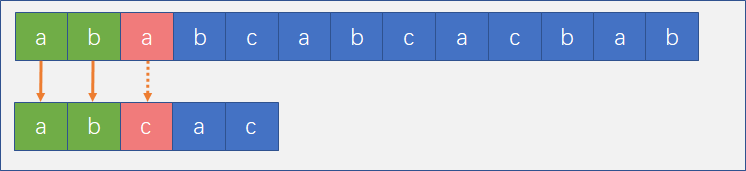
image.png
可以看到当主串进行第三个字符和子串第三个字符比较时，无法匹配成功，如果我们按照BF算法，我们会如下做：

  • 将 i 回溯到2，将 j 回溯到1
  • 继续将第主串 i(2) 个字符与子串第 j(1)个字符比较

这时候BF算法的劣势就出现了，但是其实我们发现其实 i 不用回溯也可以，因为子串的第一个字符刚好可以和第三个字符相等，所以我们可以这么比较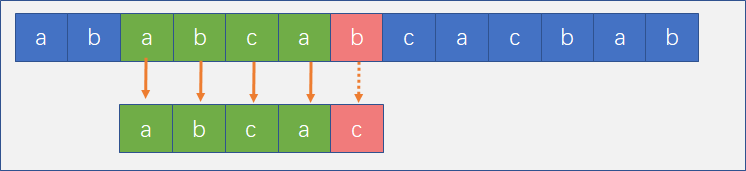
image.png
但是可以发现当主串第七位和子串第五位匹配时还是失败了，此时我们还将 i 和 j 回溯吗？同理，当然不用了，j回溯到子串的第二个字符就好了，而 i 就不用回溯了。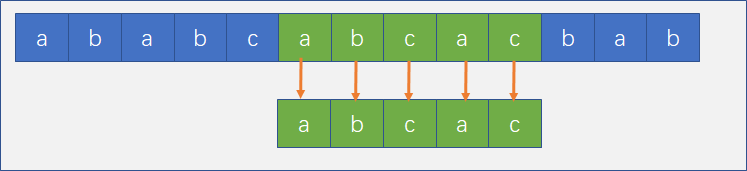
image.png
这样我们就可以做到只要回溯 j ，而不用回溯 i ，将程序的效率提升了很多，所以我们只需要找到 j 需要匹配的位置就好了，那么 j 应该怎么计算的呢？
image.png
以上为next[j]的函数，我们再通过一个例子进行讲述
image.png

  1. 当 j = 1 时，next[j] = 0
  2. 当 j = 2 时，前面只有一个字符a，所以它不属于前缀也不属于后缀，属于其他情况，next[j] = 1
  3. 当 j = 3 时，前缀a 和 后缀 b 判断是否相等，不相等属于其他情况，next[j] = 1
  4. 当 j = 4 时，前缀a 和 后缀c 判断是否相等，不等 -> 前缀ab 和 后缀bc 判断相等，不等，next[j] = 1
  5. 当 j = 5 时，前缀a 和 后缀a 判断是否相等，相等，则计算 k=n+1，此处只有一个字符重合，所以n为1，k为2，next[j] = k = 2

以上就是计算的next[j]的方法，所以我们只需要计算出next数组的内容，我们就可以根据next数组的内容，来对应j回溯的位置。
代码

  1. // 我们先计算出next数组
  2. void get_next(SqString* T, int* next) {
  3.     int i, k;
  4.     i = 1, k = 0, next[1] = 0;
  5.     // 子串从1匹配到末尾
  6.     while (i < T->length) {
  7.         // 子串的前缀和后缀进行比较，如果比较成功，i和k++，匹配多个字符
  8.         // 当不匹配时，回溯k值
  9.         if (k == 0 || T->ch[i] == T->ch[k]) {
  10.             i++;
  11.             k++;
  12.             next[i] = k;
  13.         }
  14.         else {
  15.             k = next[k];
  16.         }
  17.     }
  18. }
  1. int Index_KMP(SqString* S, SqString* T, int pos) {
  2.     int i, j;
  3.     i = pos, j = 1;
  4.     int next[255];
  5.     get_nextval(T, next);
  7.     while (i <= S->length && j <= T->length) {
  8.         if (j == 0 || S->ch[i] == T->ch[j]) {
  9.             i++;
  10.             j++;
  11.         }
  12.         else {
  13.             // i值不回溯，只回溯j即可
  14.             j = next[j];
  15.         }
  16.     }
  17.     return j > T->length ? i - T->length : 0;
  18. }

get_next函数的改进

image.png
可以发现，当子串的多个字符相等时，j 还是需要一个一个回溯，所以效率还是很低，如果多个字符相等，我们就没有必要一个个字符回溯了。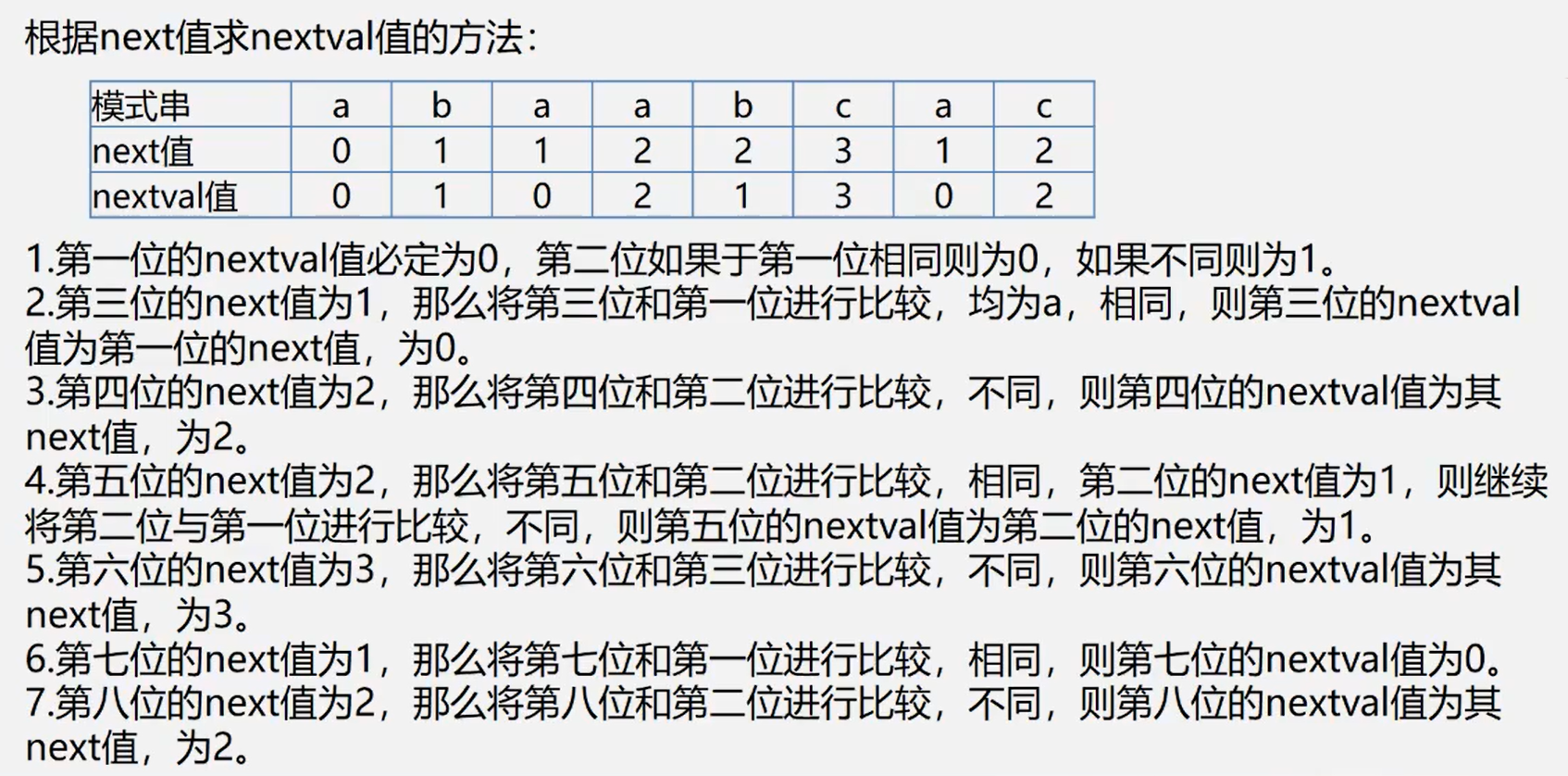
next.png
所以我们可以延伸出新的get_nextval函数：

  1. void get_nextval(SqString* T, int* nextval) {
  2.     int i, k;
  3.     i = 1, k = 0, nextval[1] = 0;
  4.     while (i < T->length) {
  5.         if (k == 0 || T->ch[i] == T->ch[k]) {
  6.             i++;
  7.             k++;
  8.             if (T->ch[i] != T->ch[k]) {    // 若当前字符与前缀字符不同
  9.                 nextval[i] = k;            // 则当前的k为nextval在i位置的值
  10.             }
  11.             else {
  12.                 nextval[i] = nextval[k];    // 反之，则将前缀字符的nextval值赋值给nextval在i位置的值
  13.             }
  14.         }
  15.         else {
  16.             k = nextval[k];
  17.         }
  18.     }
  19. }

数组

数组：按一定格式排列起来的具有相同类型的数据元素的集合
一维数组：若线性表中的数据元素为非结构的简单元素，则称为一维数组。
一维数组的逻辑结构：线性结构，定长的线性表。

二维数组：若一维数组中的数据元素有是一堆数据结构，则称为二维数组。
二维数组的逻辑结构：

  • 非线性结构：每一个元素记载一个行表中，又在一个列表中
  • 线性结构：定长的线性表，该线性表的每个数据元素也是一个定长的线性表。

三维数组：若二维数组中的元素有是一个一维数组，则称为三维数组。
n维数组以此类推…
结论：线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展
数组特点：结构固定——定义后，维度和维界不再改变。
数组基本操作：除了结构的初始化和销毁之外，只有取元素和修改元素值的操作。

数据的抽象数据类型定义

image.png
image.png

数组的顺序存储

因为数组结构固定并且一般不做插入和删除操作，所以一般都是采用顺序存储结构来表示数组。
注意：数组是可以多维的，但存储数据元素的内存单元地址是一维的，因此，在存储数组结构之前，需要解决将多维关系映射到一维关系的问题。

一维数组

例，有数组定义：int a[5];
每个元素占用4字节，假设a[0]存储在2000地址处，那么a[3]的地址就存储在43+2000=2012地址处。
所以一维数组的计算方式为
*LOC(i) =

  • LOC(0) = a -> i = 0
  • LOC(i-1)+L = a + i*L -> i > 0

二维数组

存储单元是一维结构，而数组是个多维结构，则用一组连续存储单元存放数组的数据元素就有个次序约定问题。存储二维数组时有两种存储方式：

  • 以行序为主序(低下标优先)
  • 以列序为主序(高下标优先)

以行序为主序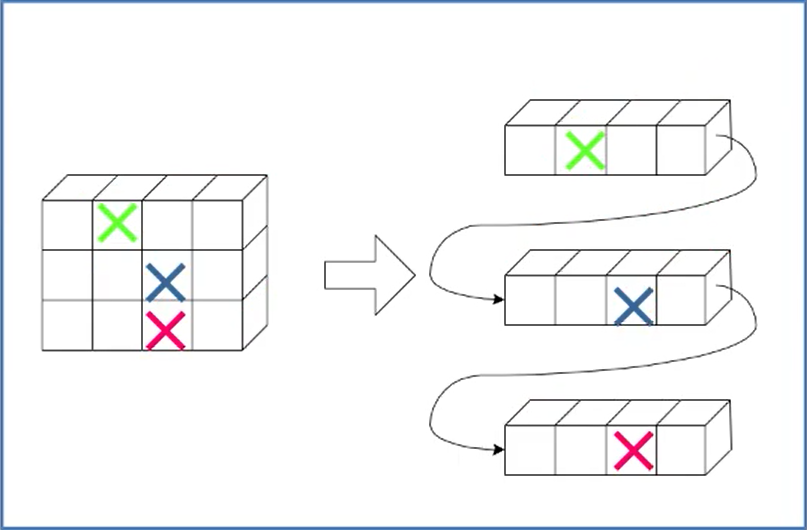
image.png
设数组的开始存储位置LOC(0,,0)，存储每个元素需要L个存储单元，数组元素a[i][j]的存储位置是：
串、数组和广义表 - 图21

以列序为主
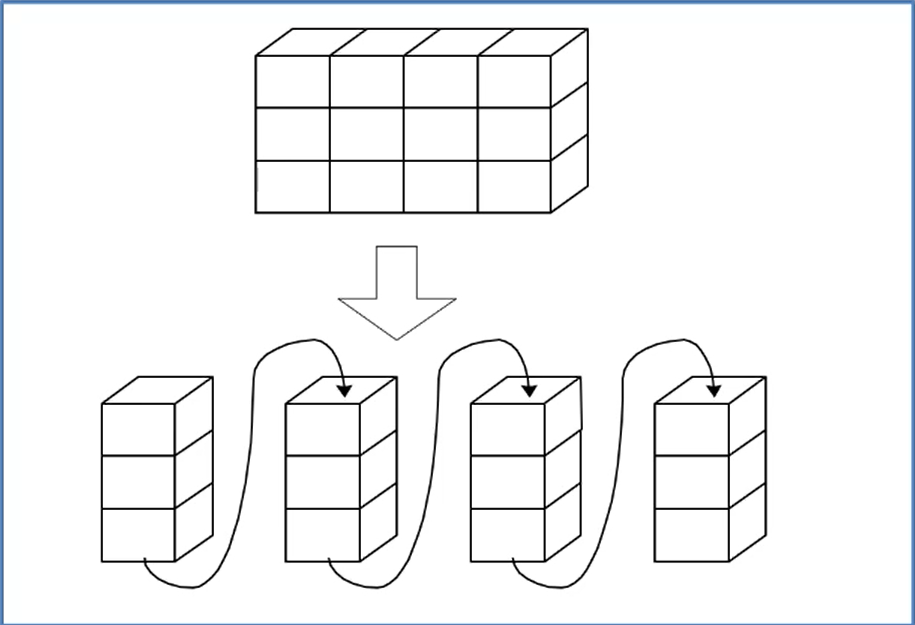
image.png

image.png

三维数组

按页/行/列存放，页优先的顺序存储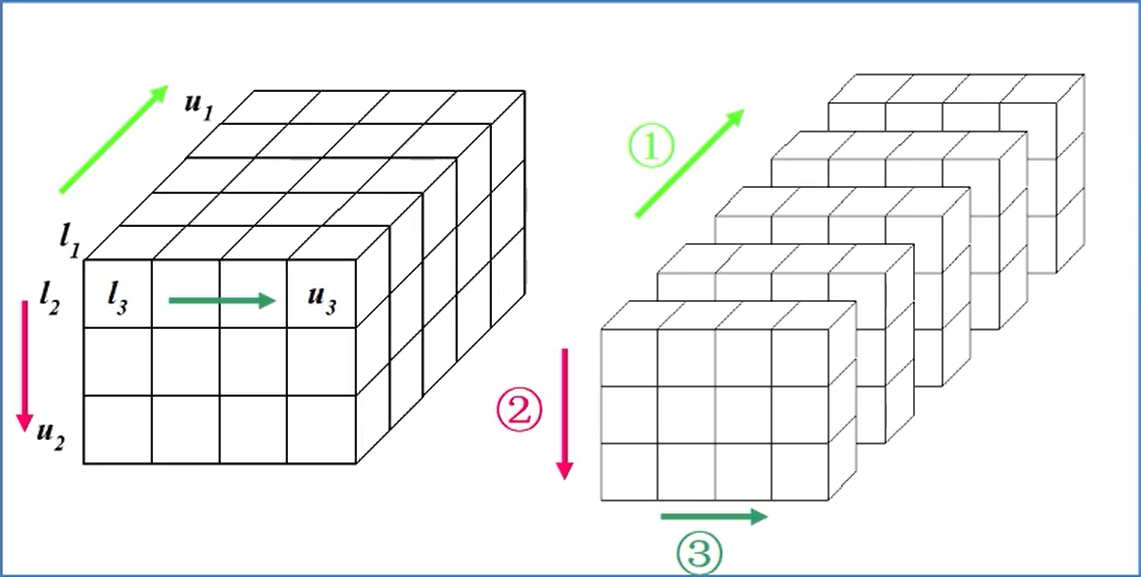
image.png
a[m1][m2][m3]各维元素个数m1,m2,m3
下标为i1，i2，i3的数组元素的存储位置：
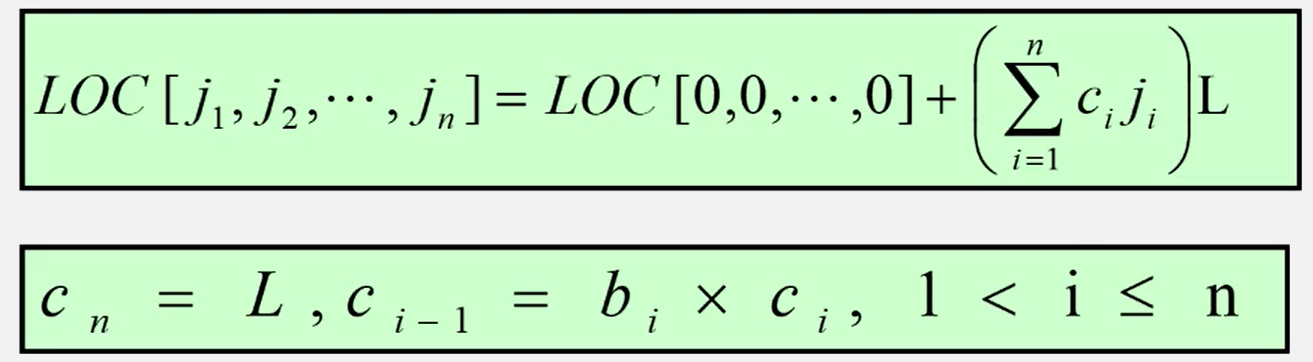
image.png

n维数组

image.png
image.png

例题

设有一个二维数组A[m][n]按行优先顺序存储，假设A[0][0]的存放位置在644(10)，A[2][2]存放位置在676(10)，每个元素占一个空间，问A[3]3存放在什么位置(脚注10)表示用10进制表示)
image.png

特殊矩阵的压缩存储

矩阵：一个由m*n各元素排成的m行n列的表。
矩阵的常规存储：将矩阵描述为一个二维数组。
矩阵的常规存储特点：可以对其元素进行随机存取；矩阵运算非常简单；存储的密度为1
不适宜常规存储的矩阵：值相同的文输很多呈某种规律分布，零元素多。
矩阵的压缩存储：为多个相同的非零元素只要分配一个存储空间；对零元素不分配空间。
什么样的矩阵能够压缩：一些特殊的矩阵，如：对称矩阵、对角矩阵、三角矩阵、稀疏矩阵等
什么叫稀疏矩阵：矩阵中非零元素的个数较少(一般小于5%)

对称矩阵

特点：在n*n的矩阵a中和，满足如下性质：aij=aji(1<=i,j<=n)，如下图a[1][0] = a[0][1] = 5
存储方法：只存储下(或者上)三角(包括主对角线)的数据元素，共占用n(b+12)/2各元素空间。
image.png
对称矩阵的存储结构：对称矩阵上下三角中的元素数均为：n(n+1)/2
可以以行序为为将元素存放再一个一维数组 sa[n(n+1)/2] 中：
例如：以行序为主序存储下三角：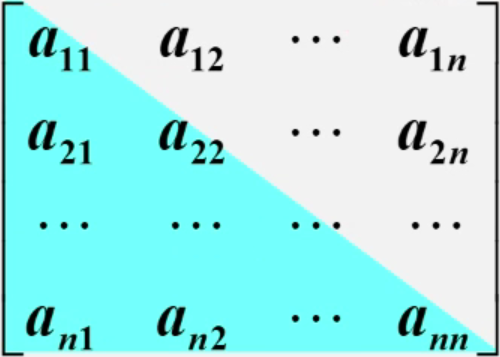
image.png
image.png

三角矩阵

特点：对角线以下(或以上)的数据元素(不包括对角线)全部为常数c。
image.png
存储方法：重复元素C共享一个元素的存储空间，共占用n(n+1)/2+1个元素空间：sa[1 … n(n+1)/2+1]
image.png

对角矩阵

特点：在nn的方阵中，所有非零元素都集中在以主对角线为中心的·带状区域，区域外1的值全为0，则称为对角矩阵。常见的有三对角矩阵，五对角矩阵、七对角矩阵等。
如图所示，为一个77的三对角矩阵：
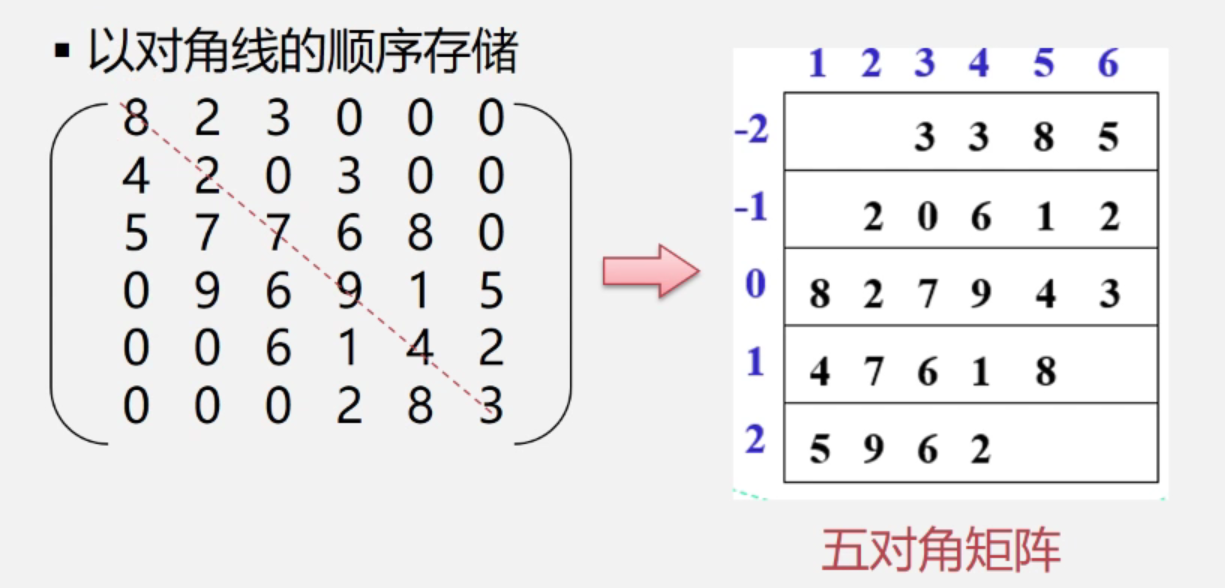
image.png
存储方法
image.png

稀疏矩阵

设在一个mn的矩阵中有t个非0元素，令 y = t/(mn)，当y <= 0.05时称为稀疏矩阵，如下图：
image.png

存储方法

三元组存储
三元组(i,j,aij)唯一确定矩阵的一个非0单元。
压缩存储原则：存各非0元素的值，行列位置和矩阵的行列数
三元组的不同表示方法可以决定稀疏矩阵不同的压缩存储方法
image.png
注意：为更可靠描述，通常再加一个”总体”信息在第0行，即总行数、总列数、非零元素总个数

例题：试还原出下列三元组所表示的稀疏矩阵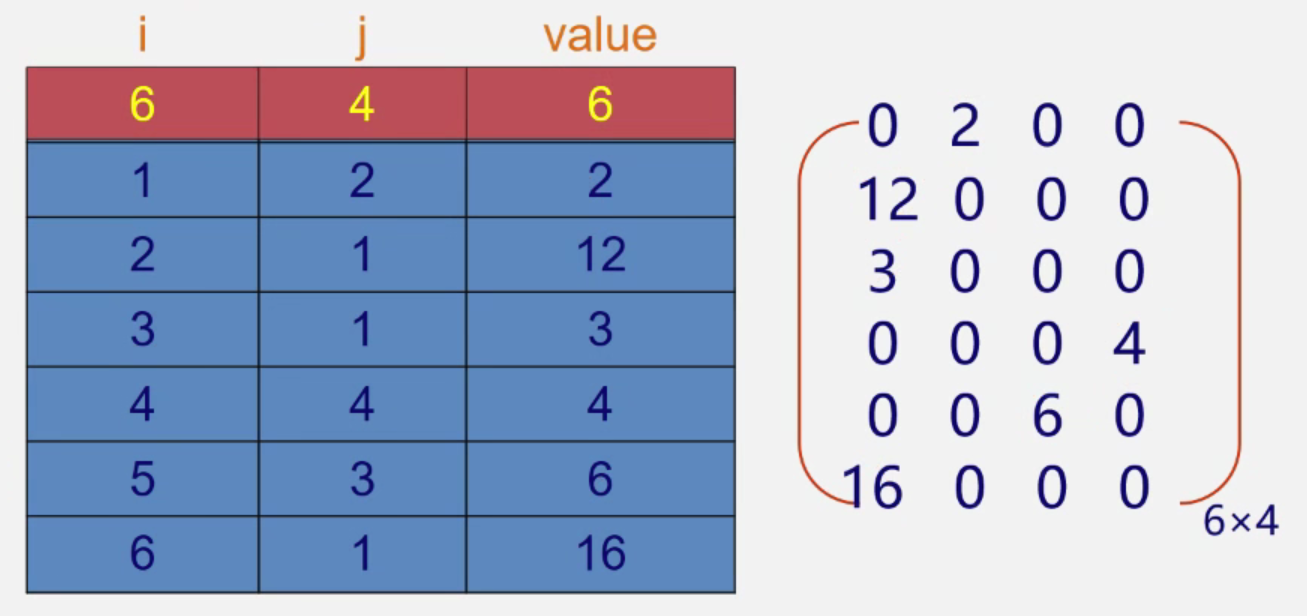
image.png

三元组顺序表又称有序的双下标法。
三元组顺序表的优点：非0元素在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算。
三元组顺序表的缺点：不能随机存取，若按行号存取某一行中的非0元素，则需从头开始查找

三元组的链式存储结构：十字链表
在一个十字链表中，矩阵的每一个非0元素用一个结点表示，该接待你除了(row，col，value)以外，还要两个域：

  • right：用以链接同一行中的下一个非0元素。
  • down：用以链接同一列中的下一个非0元素。

十字链表结构示意图：
image.png
优点：它能够灵活的插入因运算而产生的新的非0元素，删除因运算而产生的新的0元素，实现矩阵的各种运算。

【例题】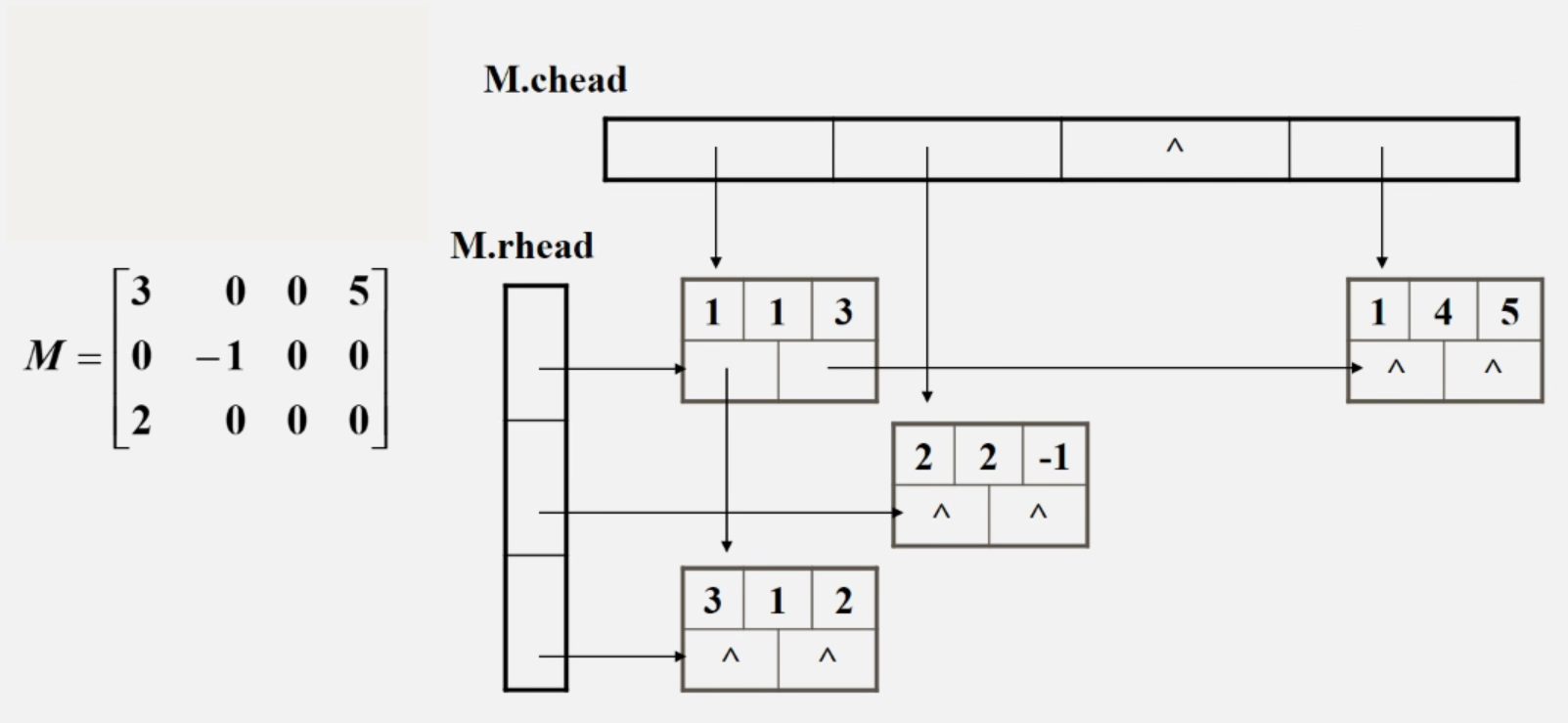
十字链表.png

广义表

广义表(又称列表Lists)是 n>=0 个元素 a0，a1，… , an-1的有限序列，其中每一个ai或者是原子，或者是一个广义表。
广义表通常记作：串、数组和广义表 - 图41，其中LS为表名，n为表的长度，每一个ai为表的元素。
习惯上，一般用大写字母表示广义表，小写字母表示原子。
表头：若LS非空(n>=1)，则其第一个元素 a1就是表头。记作head(LS)=an-1。注意：表头可以是原子，也可以是子表。
表尾：除表头之外的其他元素组成的表。记作tail(LS)=(a2，… , an)。注意：表尾不是最后一个元素，而是最后一个子表。
广义表.png

广义表的性质

  1. 广义表中的数据元素有相对次序：一个直接前驱和直接后继，表头无前驱，表尾无后继。
  2. 广义表的长度定义为最外层所包含元素的个数。如：C = (a,(b,c)) 是长度为2的广义表。
  3. 广义表的深度定义为该广义表展开后所包含括号的重数。如：A = (b,c)的深度为1，B=(A.d)的深度为2，C = (f,B,h)的深度为3。注意：原子的深度为0，空表的深度为1.
  4. 广义表可以为其他广义表共享；如上：广义表B就共享表A。
  5. 广义表可以是一个递归的表。如：F=(a,F)。注意：递归表的深度是无穷值，长度是有限值
  6. 广义表是多层次结构，广义表的元素可以是单元素，也可以是子表，而子表的元素还可以是子表。可以用图形象的表示

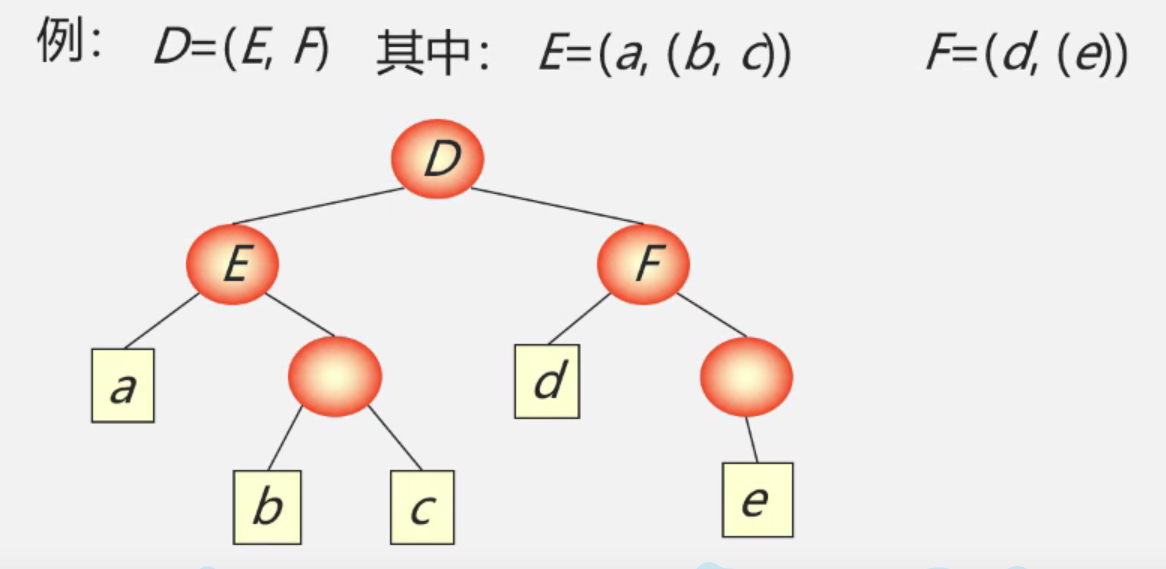
image.png

广义表和线性表的区别

广义表可以看成是线性表的推广，线性表是广义表的特例。广义表的结构相当灵活，再某种前提下，它可以兼容线性表，数组，树和有向图等各种常用的数据结构。

广义表的基本运算

  1. 求表头：GetHead(L)，非空广义表的的第一个元素，可以是一个原子也可以是一个子表。
  2. 求表尾：GetTail(L)，非空广义表除去表头元素以外其他元素所构成的表，表尾一定是个表。

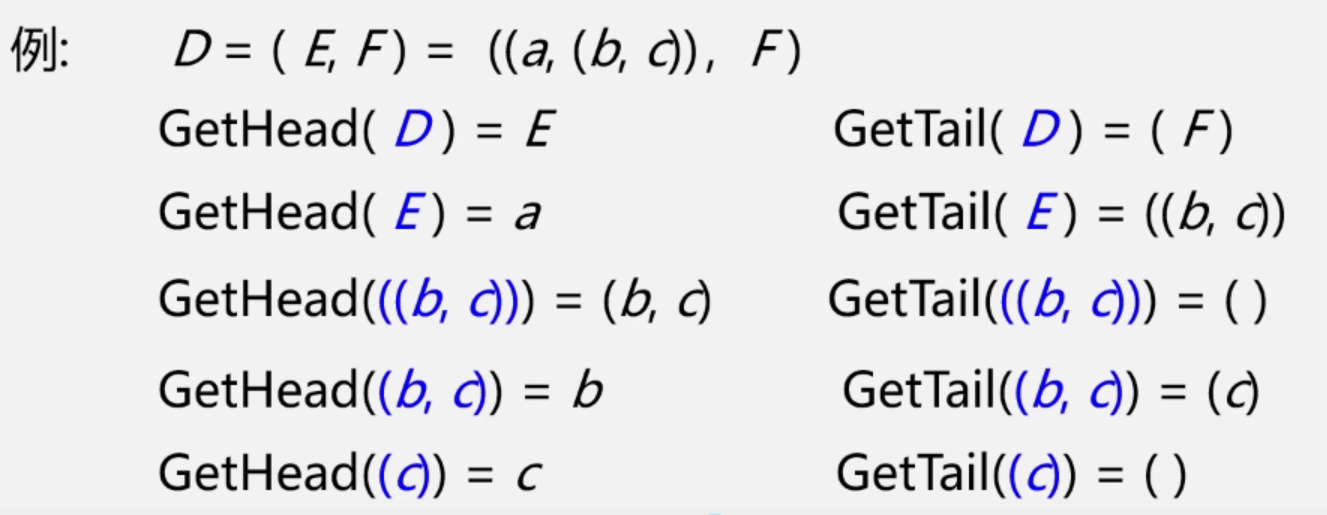
image.png

案例分析

病毒感染检测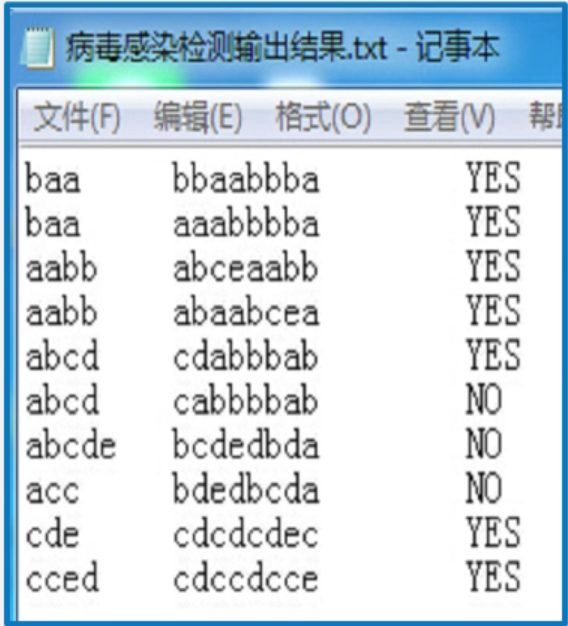
image.png
我们学习了BF算法和KMP算法，所以我们只需要再主串中匹配子串即可。
但是这里的问题还是有些特殊，因为病毒是环状结构，所以假设有一个病毒是baa，那么以下三种形式的子串也是它：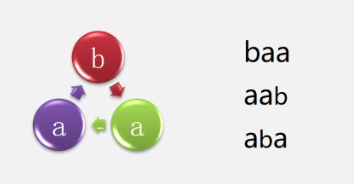
image.png
所以为了让各种情况都能匹配，所以我们向内存申请2m(m为子串长度)的空间，如”baa”，我们在内存中可以设置为”baabaa”，然后我们每次匹配m个字符，然后从下一个位置再匹配m个字符，执行m此循环，就可以解决我们的需求