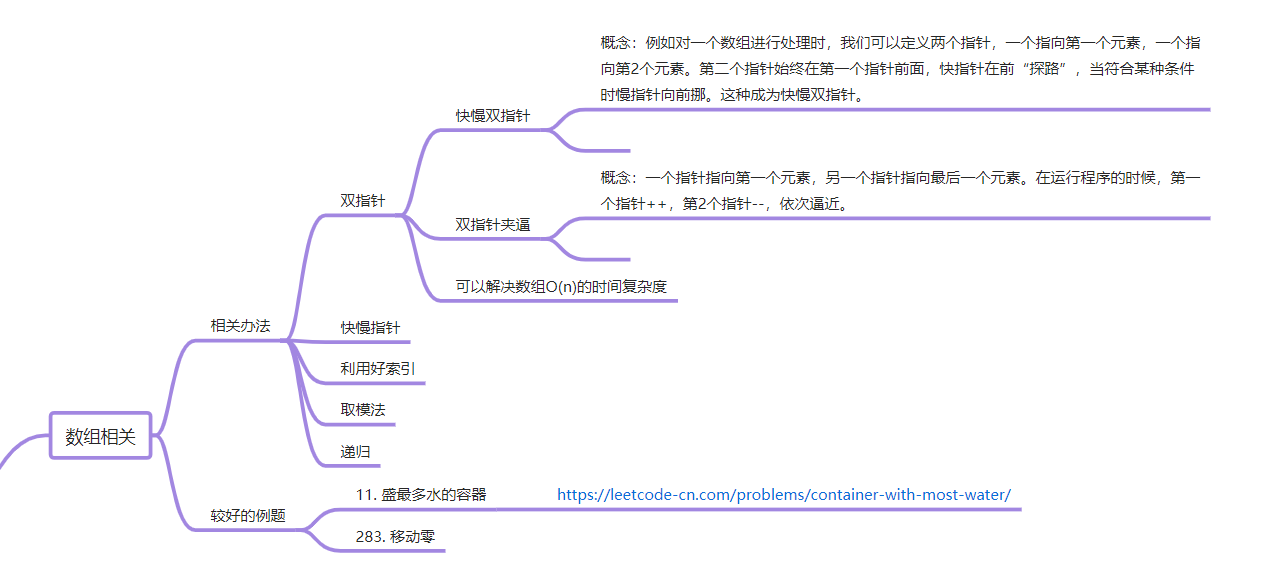
快慢双指针经常用来解决数组在遍历的过程中时间复杂度是O(n)的情况。
11. 盛最多水的容器
示例 1:
**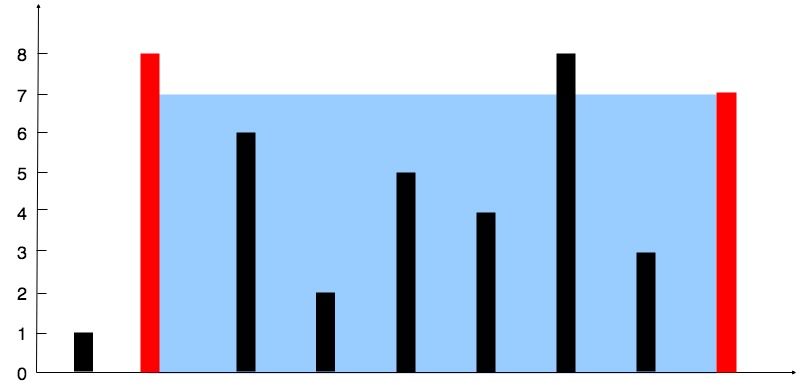
输入:[1,8,6,2,5,4,8,3,7]输出:49解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1]
输出:1
示例 3:
输入:height = [4,3,2,1,4]
输出:16
示例 4:
输入:height = [1,2,1]
输出:2
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/container-with-most-water
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
根据生活常识,木桶能盛水的水量,取决于最短的一块板子,如下图所示:
可以先给这个示例进行一个编号:
1-9号
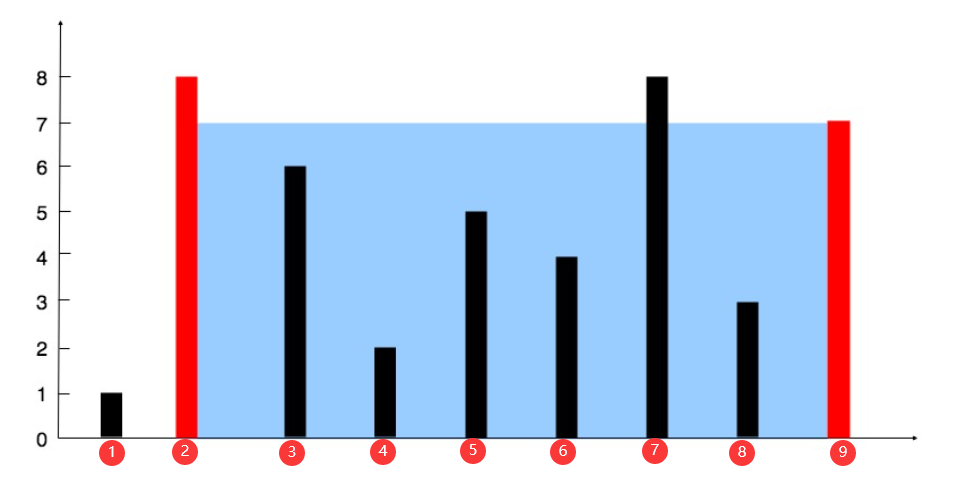
怎么才能找到盛水最多的容器呢?肯定是取决于板子的高低。
如果我们拿①号板子到⑨号板子来说的话:
①号板子的高度是1; ⑨号板子的高度是7; 那么这个范围的成水量就取决于①号板子的高度,因为在①和⑨号板子中,①号板子的高度是最低的。
如果我们拿②号板子到⑨号板子来说的话: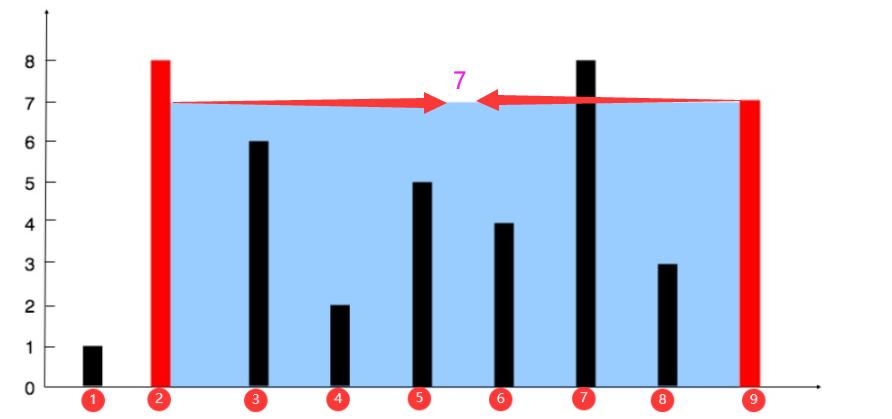
②号板子的高度是8; ⑨号板子的高度是7; 那么这个范围的成水量就取决于⑨号板子的高度,因为在②和⑨号板子中,⑨号板子的高度是最低的。
这个范围的盛水量是:7(高)* 7(宽)=49。
这道算法题就是让我们找出可以盛水最多的容器,那么很明显,这个图中的最大值就是49。
在业界通常流传着一句话:往往第一次想到的解决办法都不是最好的,或者说都不是最优的。
能解决这道算法题有很多种办法,例如我们可以穷举每一块板子到其他所有板子的最大值。最终也可以拿到结果,无非就是复杂度高一点。
暴力解法
如下代码:
在下面这段暴力解法中,可以看到思路还是挺简单的,就是对每一根板子进行遍历,求出来每一个板子与其他所有板子的区域面积,最终选取最大的一个面积。
class Solution {
public int maxArea(int[] height) {
int max = 0;
for(int i = 0;i<height.length;i++){
//j = i+1 ;这里为什么要i+1呢?因为是不让重复的走自己走过的路
for(int j = i+1 ; j < height.length;j++){
int high = Math.min(height[i],height[j]);//选出最小的板子的高度
int wide = j - i;//宽
int area = high * wide;//容量面积 = 高 * 宽
max = Math.max(area,max);//保留最大值的容量
}
}
return max;
}
}
但是我们可以看到,虽然能顺利的解出这道题,但是时空复杂度是不这么完美的。如果你是一个追求完美的人,可能就需要进行一番折腾去想办法去优化了。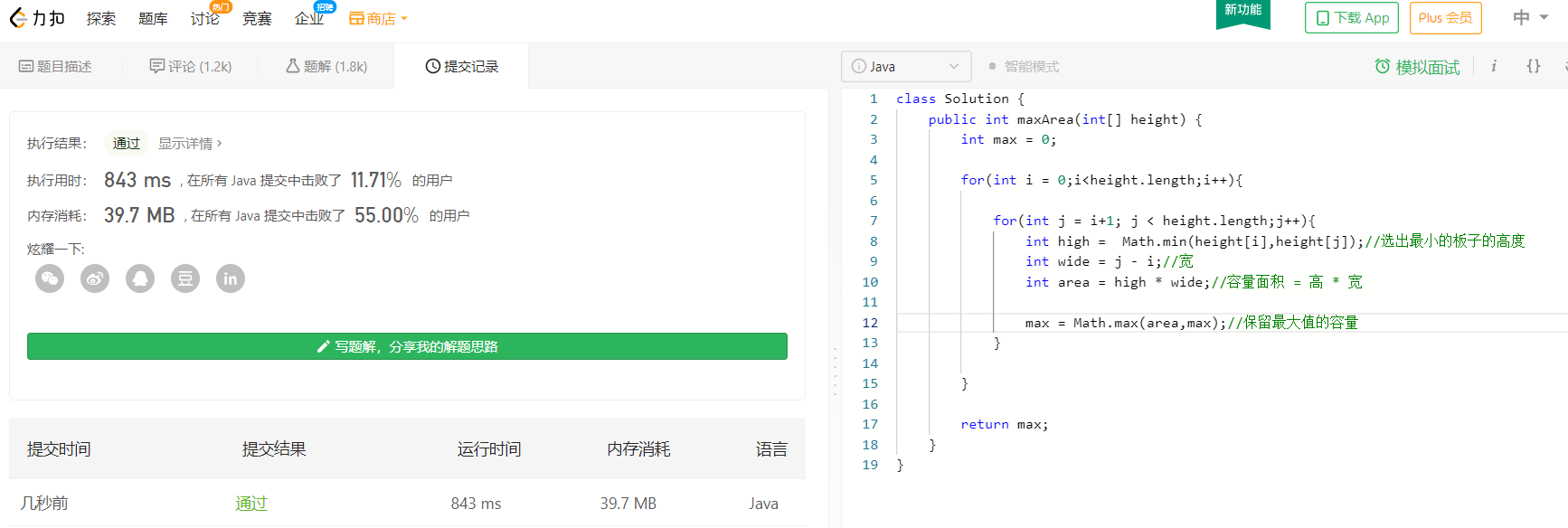
双指针
代码如下:
我们定义两个指针,一个指向数组的头,一个指向数组的尾。 然后 头—-> 逐渐逼近<——尾
class Solution {
public int maxArea(int[] height) {
//定义双指针
int i = 0;//指针一,指向头
int j = height.length - 1;//指针二,指向尾
int max = 0;//记录最终最大的值
while(j -i >=1){
max = Math.max(Math.min(height[i],height[j]) * (j-i),max);
//移动缩小范围
if(height[i] <= height[j] ){
i++;//指针一向后移动
}else{
j--;//指针二向前移动
}
}
return max;
}
}
经过我们的优化,可以看到已经有效果了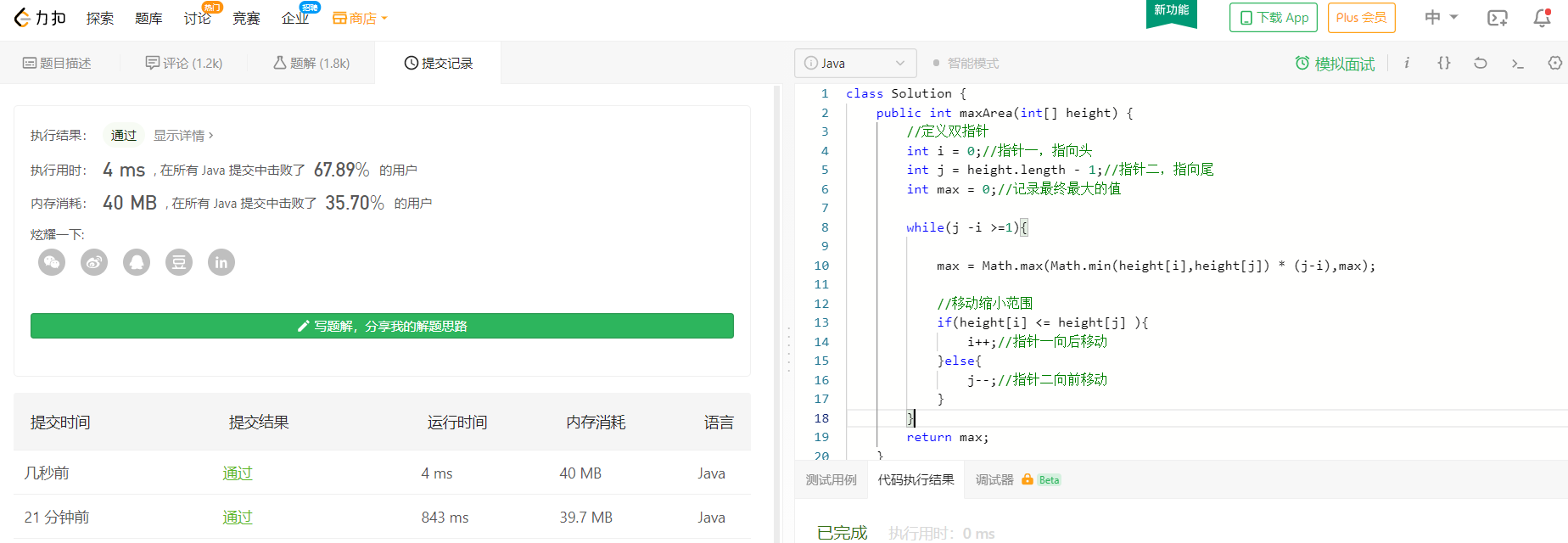
1. 两数之和
为了更详细的说明接下来的问题,先拿出两数之和这个题目来说一下。
题目如下:
//给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
//
// 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
//
//
//
// 示例:
//
// 给定 nums = [2, 7, 11, 15], target = 9
//
//因为 nums[0] + nums[1] = 2 + 7 = 9
//所以返回 [0, 1]
//
// Related Topics 数组 哈希表
// 👍 9725 👎 0
链接:https://leetcode-cn.com/problems/two-sum
这个题我们可以使用暴力手段:
思路还是很明确的,当nums[i] + nums[j] = target时,即可返回i和j坐标
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length - 1; i++) {
for (int j = i+1; j < nums.length ; j++) {
if(nums[i] + nums[j] == target){
return new int[]{i,j};
}
}
}
return new int[]{};
}
可以看到虽然是暴力的手段,单纯的看着效果还是挺不错的。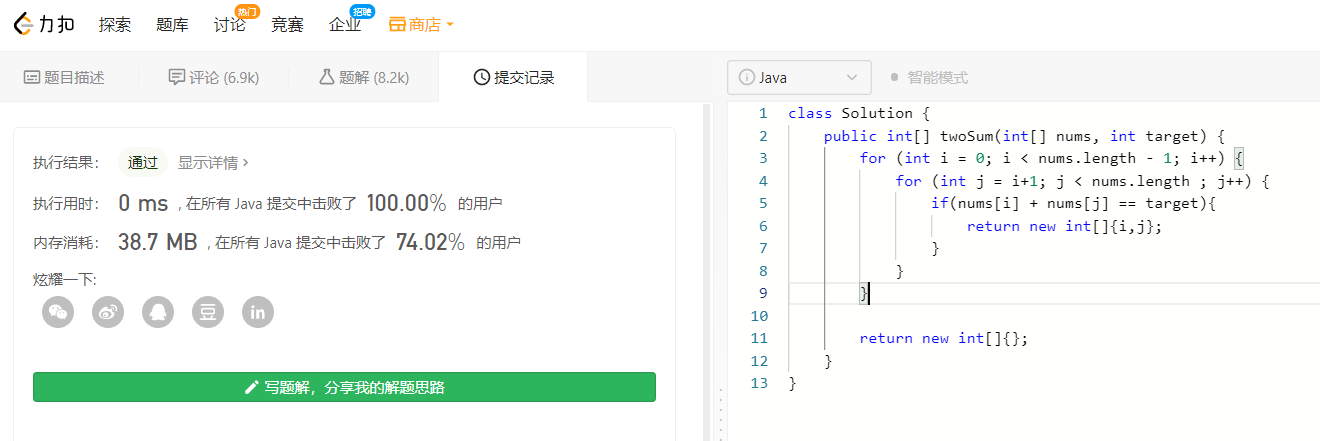
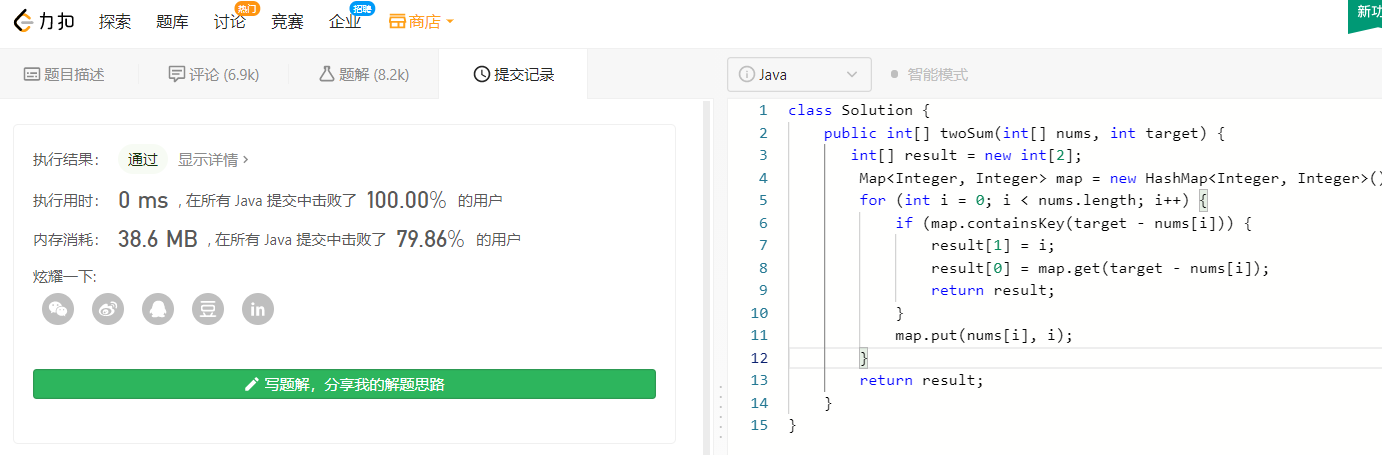
那么有没有优化的可能性呢,答案是有的,例如:可以使用hash表来存储。
public int[] twoSum(int[] nums, int target) {
int[] result = new int[2];
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int i = 0; i < nums.length; i++) {
if (map.containsKey(target - nums[i])) {
result[1] = i;
result[0] = map.get(target - nums[i]);
return result;
}
map.put(nums[i], i);
}
return result;
}
15. 三数之和
题目:
//给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复
//的三元组。
//
// 注意:答案中不可以包含重复的三元组。
//
//
//
// 示例:
//
// 给定数组 nums = [-1, 0, 1, 2, -1, -4],
//
//满足要求的三元组集合为:
//[
// [-1, 0, 1],
// [-1, -1, 2]
//]
//
// Related Topics 数组 双指针
// 👍 2785 👎 0
力扣链接:https://leetcode-cn.com/problems/3sum
暴力解法
对于二数之和的题目,我们可以
当nums[i] + nums[j] = target时,即可返回i和j坐标
那么此题中三数之和,我们肯定也可以类似二数之和的做法一样会去做:
1、三重for循环遍历nums数组; 2、找到nums[i]+nums[j]+nums[k] = 0 保存nums[i],nums[j],nums[k]; 3、继续寻找; 4、返回保存的数据即可。
那么上面这个思路就是暴力的手段了。
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
int len = nums.length;
//利用set去重
Set<List<Integer>> set = new HashSet<>();
for (int i = 0; i < len; i++) {
for (int j = i+1; j < len; j++) {
for (int k = j+1; k < len; k++) {
if(nums[i]+nums[j]+nums[k] == 0){
List<Integer> list = new ArrayList<>();
list.add(nums[i]);
list.add(nums[j]);
list.add(nums[k]);
Collections.sort(list);
set.add(list);
}
}
}
}
return new ArrayList<>(set);
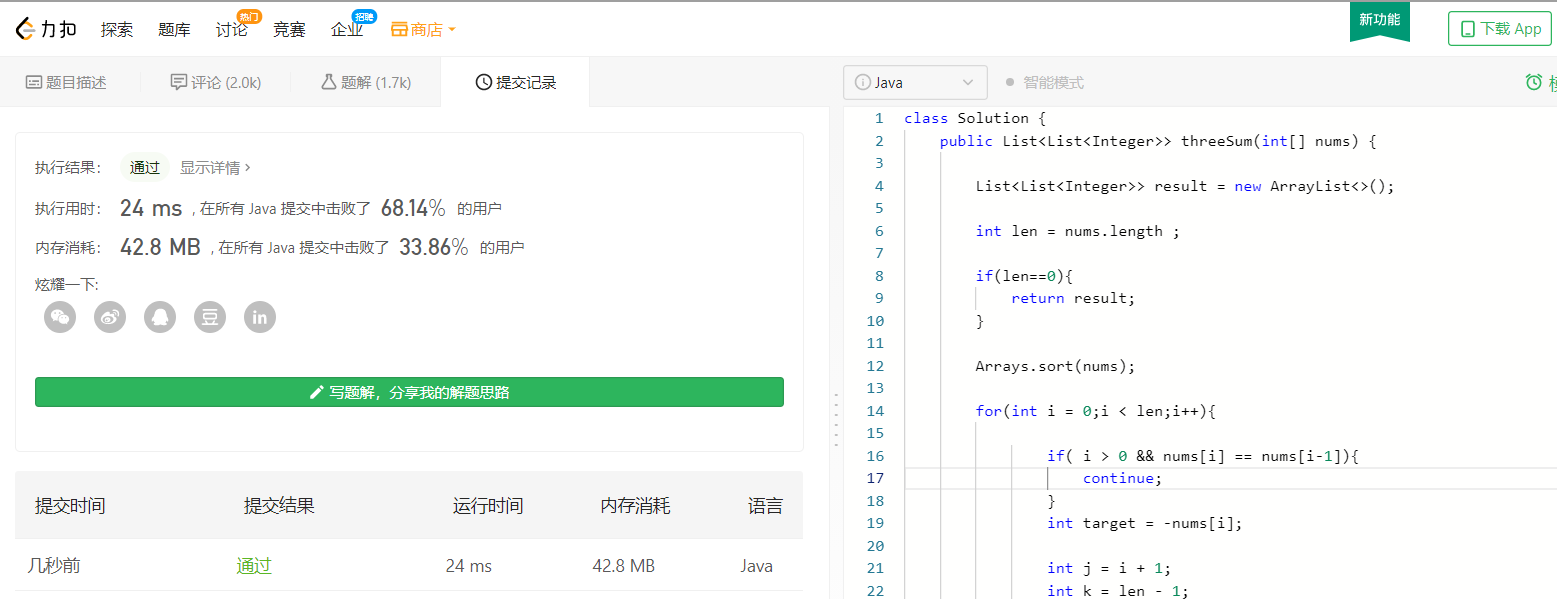
}
很遗憾的是,暴力解法跑不过测试程序,超时了:
双指针解法
双指针可以解决数组相关算法题的大多数超时问题。
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
//如果传递的数组是空的,直接返回一个空的list集合
if(nums.length == 0) return result;
//排序
Arrays.sort(nums);
int len = nums.length;
//遍历
for (int i = 0; i < len; i++) {
//跳过重复的值
if(i>0 && nums[i] == nums[i-1])
continue;
/**
* a=i
* b=j
* c=k
*
* 因为:a+b+c=0
* 那么:b+c=-a
* 那么nums[j] + nums[k] = -nums[i]
*
*/
int target = -nums[i];//目标数
int j = i +1;//头指针
int k = len - 1;//尾指针
//两个指针到中间相遇了,既结束
while ( j < k){
//判断 b+c = -a 是否成立
if(nums[j] + nums[k] == target){
//组装数据
List<Integer> curr = new ArrayList<>();
curr.add(nums[i]);
curr.add(nums[j]);
curr.add(nums[k]);
//添加到结果集
result.add(curr);
//移动头指针和尾指针,缩小范围
j++;
k--;
//进一步减小范围
//1、检查左边
while (j < len && nums[j] == nums[j - 1]) j++;
//2、检查右边
while (k > j && nums[k] == nums[k + 1]) k--;
//如果符合b+c > -a
/*
例如:[-4,-1,-1,0,1,2]
a=-4
b=-1
c=2
i j k
↓ ↓ ↓
a b c
↓ ↓ ↓
max data index(j) → [-4,-1,-1,0,1,2] ← min data index(k)
b+c=-1 != --4(4)
说明b+c太大了,所以我们要让b+c变小,那么就必须缩小大头
因为k指针是指向的数组中最大的一个范围,那么就需要缩小k所指的位置
则:k--
*/
}else if(nums[j] + nums[k] > target){
k--;
}else{
//反之,j++;增大数据
j++;
}
}
}
return result;
}
代码虽然比之前复杂了点,但是效果是很好的: