离散型随机变量的分布模型：
    几何分布：几何分布的详解

    二项分布：
    二项分布的特点：

    1. 做某件事的次数是固定的
    2. 每一件事情都有两个可能的结果
    3. 每一次成功的概率都是相等的
    4. 感兴趣的是成功n次的概率
    5. 0-1分布是二项分布的一个特例。

    理解样例：
    每一台机床损坏的概率为 P = 0.01，求1个人看20台、三个人看80台 不能及时维修的概率：
    分析：1. 为什么能被看成是二项分布呢？

    1.   1. 每一台机床的损坏概率是相同的。
    2.   1. 我们关心的是同一时间内，失败n次的概率（同时损坏n个机床的概率）。
    4. 2. 分析：明确什么时候才是不能维修的临界条件，然后用逆向思维的方式去思考问题，进行套公式求解即可。应该多分析，为什么能被看作是二项分布。

    泊松分布：
    用于近似计算二项分布；
    计算方式：一般无法直接计算，需要通过查泊松分布表得到结果。
    特点：

    1. 事件是独立事件。
      1. ex：独立事件：在总的样本空间中，一个事情的发生不影响其他事件的发生。
    2. 在任意相同的时间范围内，事件发生的概率相同。
    3. 预期是获取某个指定的时间范围内，发生某件事情n次的可能性有多大。

    公式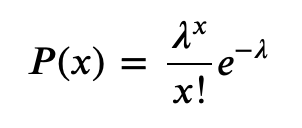：image.png，解释：x代表事件发生的次数，u代表给定事件范围内事件发生的平均次数。

    案例1：已知某个抽奖活动，一天内中奖的平均次数为 5 个，想知道一天内恰巧中奖次数为 7 的概率为多少？
    u = 5，x = 7，带公式或者利用python、R语言求解（现成的工具包）

    案例2：某非传染病发病率为 0.001，某单位5000人，至少2人得病的概率。
    分析：

    1. 做某件事的次数是固定的（最多5000人得病）
    2. 每一次成功的概率都是相等的：0.001
    3. 感兴趣的是成功n次的概率（至少2人发病的概率）
    4. 综上分析，该数据集满足二项分布。

    P = 1 - P(x = 0) - P(x = 1)
    综上所述，为了简化二项分布的计算公式，使用泊松分布进行计算，首先判断是否满足泊松分布的规律。
    通常情况下，n >= 100 and np <= 10情况下才能使用泊松分布近似计算二项分布。本题里，n = 5000，np = 5，满足近似计算的使用条件。查表计算即可。

    案例3：证券部门有1000个账户，每个账户有10万元，用户提20%的概率为0.006，问银行应该准备多少现金才能以95%的概率满足用户的提款要求。
    分析：

    1. 如何才能满足用户的提款需求？让所有用户需要提款的金额总数小于等于银行准备的钱数才行。
    2. 以每天提前的用户数为X，每天最大来的用户数为1000，每个用户提款的可能行为0.006，建立二项分布X~B(1000, 0.6)
    3. 按照分析1，建立不等式：P{2X <= x} >= 0.95（每天每个用户的提款数为2万元，X个用户，总价为2X万元）
    4. 得到P{X <= x / 2} >= 0.95，转化为了二项分布的概率公式
    5. 条件满足泊松分布近似计算二项分布，查表求出x

    超几何分布：

    连续型随机变量的分布模型：

    均匀分布：若连续型随机变量的概率密度函数为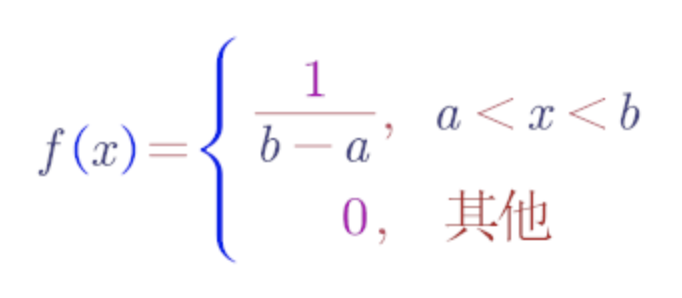：image.png
    则称随机变量x在区间（a, b）上遵循均匀分布，记为 X ~ U(a, b)

    指数分布：需要理解指数分布的无记忆性。

    正态分布：
    使用比较广泛。