什么是强连通分量

强连通分量是有向图的一部分。

两个顶点强连通：在有向图G中，如果两个顶点vi, vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从 vj 到 vi 的有向路径，则称两个顶点强连通(strongly connected)。
强连通图：如果一个有向图G，对于其中任意两个顶点v,u，都存在从v到u以及从u到v的有向路径，则称G为强连通图。
强连通分量：有向图G的极大强连通子图S，即添加任意顶点都会导致S失去强连通的属性，则称S为G的强连通分量。

例如：
让我们来看看下面的图表。


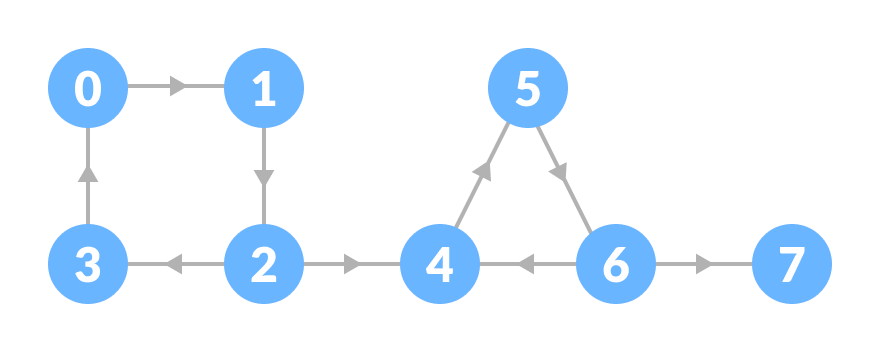
初始图

上图的强连通分量是：


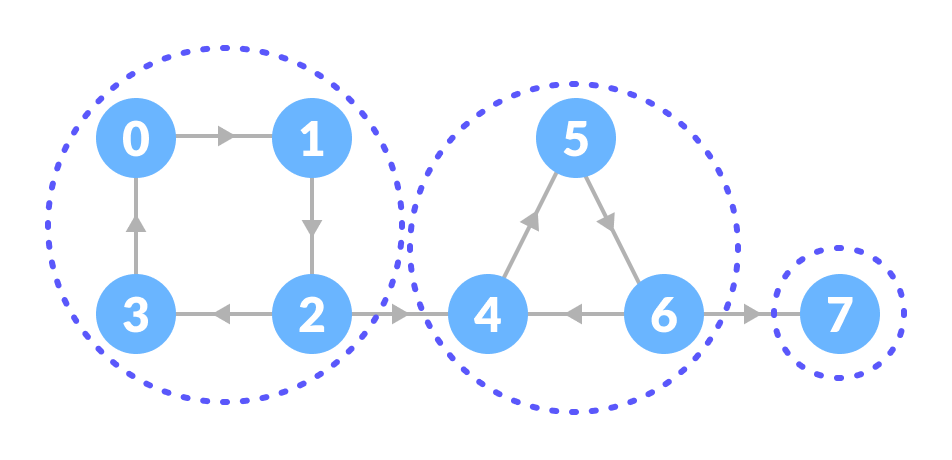
强连通分量

可以观察到，在第一个强连通分量中，每个顶点都可以通过有向路径到达另一个顶点。这些分量可以使用Kosaraju’s Algorithm找到。

Kosaraju 算法图解

Kosaraju’s Algorithm 基于两次实现的深度优先搜索算法。

涉及三个步骤：

对整个图执行深度优先搜索。

让我们从顶点 0 开始，访问它的所有子顶点，并将访问过的顶点标记为完成。如果一个顶点指向一个已经访问过的顶点，则将该顶点推入堆栈。
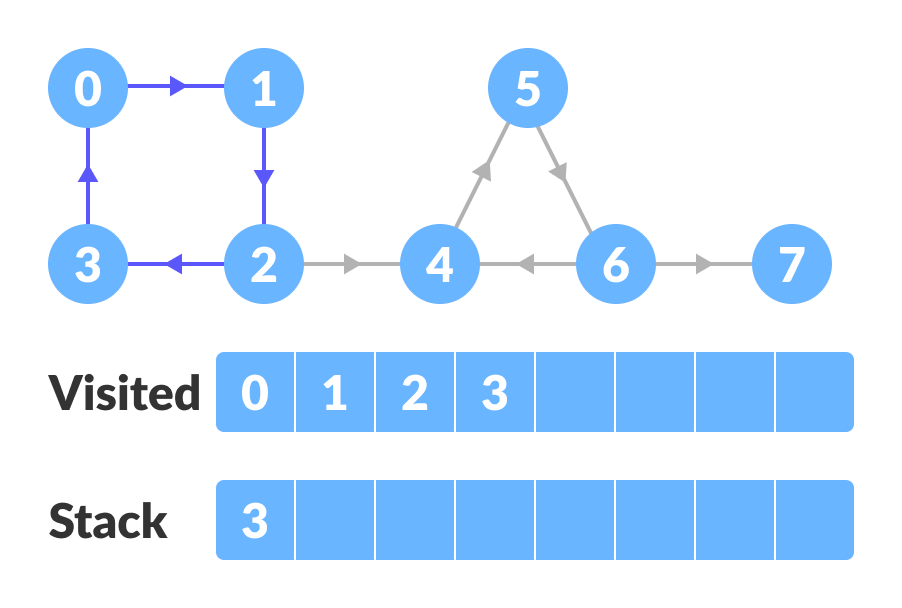
例如：从顶点0开始，到顶点1，顶点2，再到顶点3。Vertex-3 导致已经访问过的 vertex-0，因此将源顶点（即 vertex-3）压入堆栈。


图上的DFS

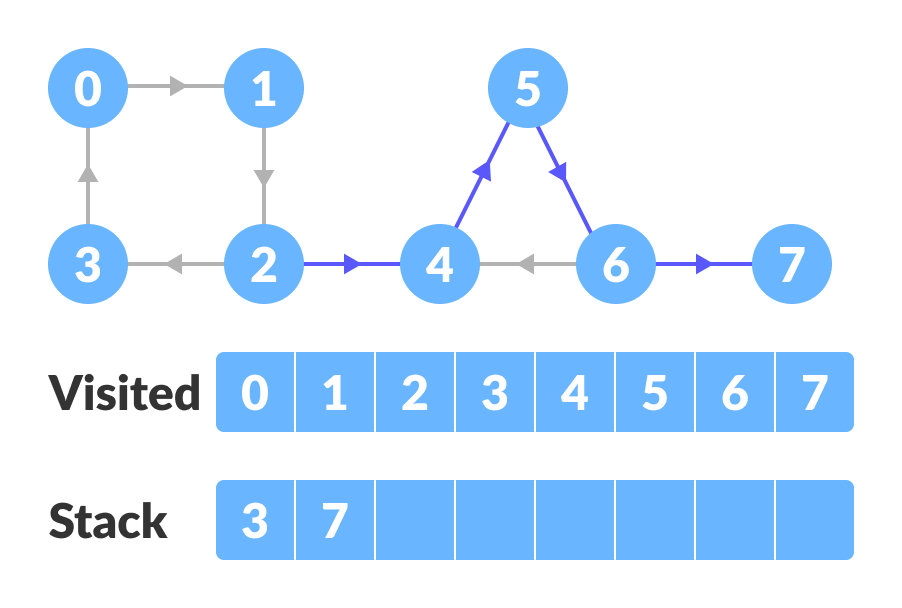
转到前一个顶点（vertex-2）并依次访问其子顶点即vertex-4、vertex-5、vertex-6和vertex-7。由于顶点 7 无处可去，将其压入堆栈。


图上的DFS

转到上一个顶点（vertex-6）并访问其子顶点。但是，它的所有子顶点都被访问了，所以将它压入堆栈。


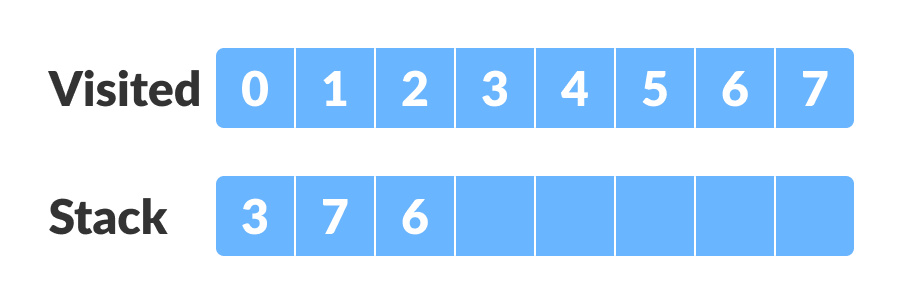堆叠

类似地，创建了最终堆栈。


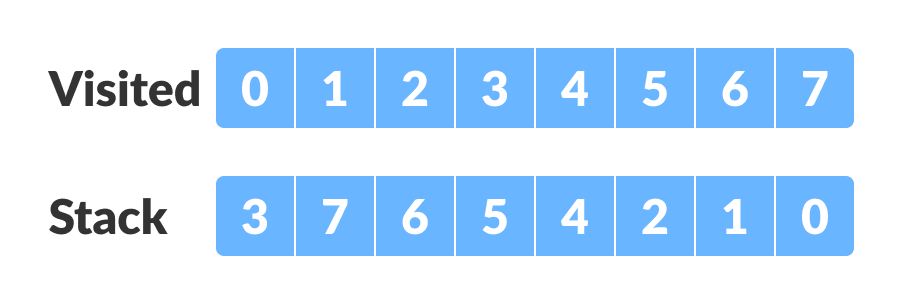最终堆栈

反转原始图形。 | 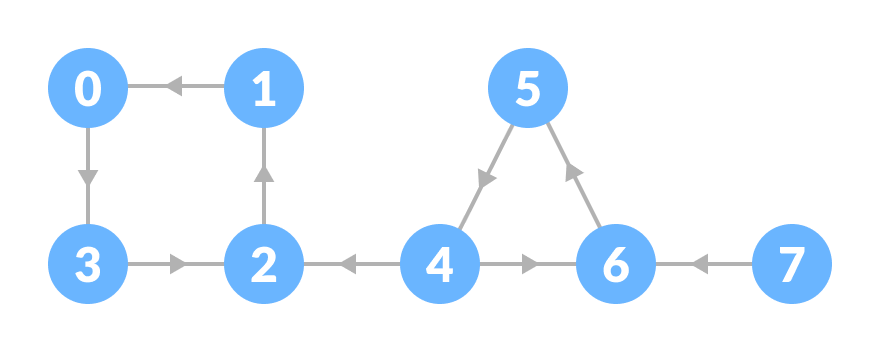| | —- | | 反向图上的 DFS |

在反转图上执行深度优先搜索。

从堆栈的顶部顶点开始。遍历其所有子顶点。一旦到达已经访问过的顶点，就形成了一个强连通分量。
例如：从堆栈中弹出顶点 0。从顶点 0 开始，遍历其子顶点（依次为顶点 0、顶点 1、顶点 2、顶点 3）并将它们标记为已访问。顶点 3 的子节点已经被访问过，所以这些访问过的顶点形成一个强连接组件。


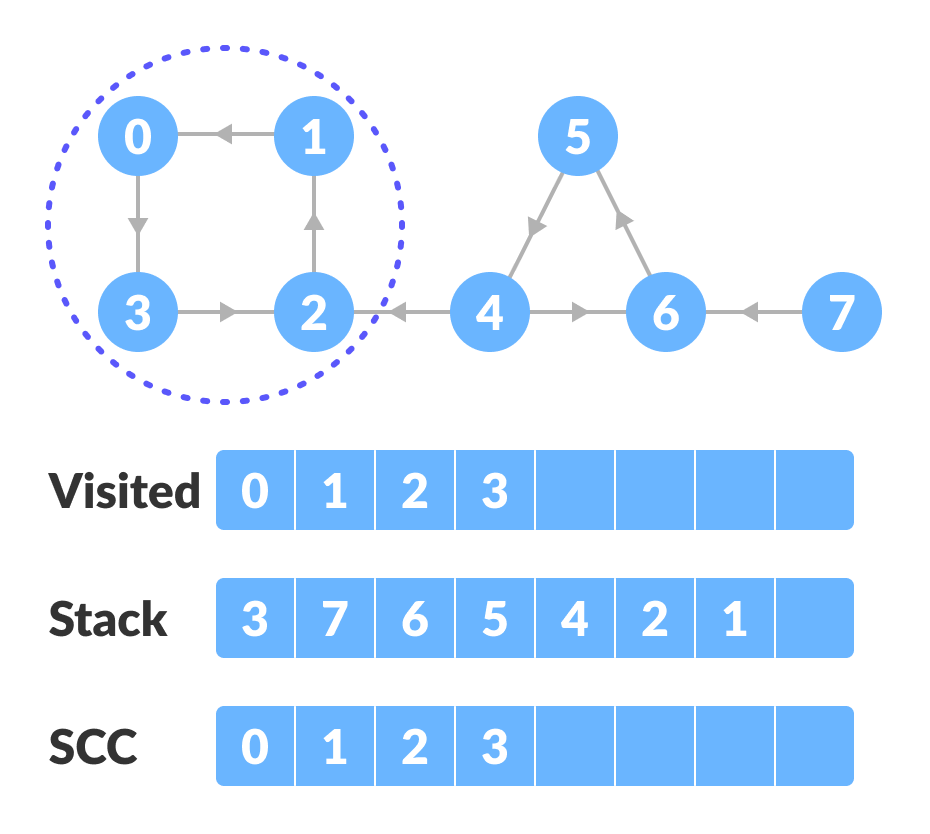从顶部开始，遍历所有顶点

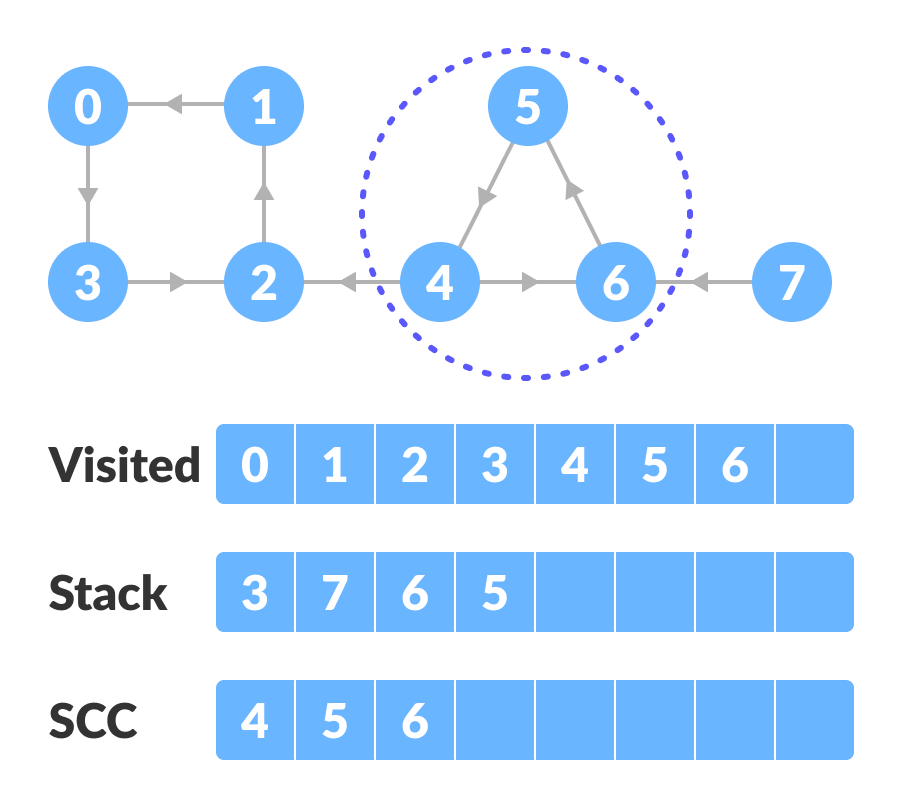
如果已经访问过，则转到堆栈并弹出顶部顶点。否则，从堆栈中选择顶部顶点并遍历其子顶点，如上所示。


如果已经访问过，则弹出顶部顶点


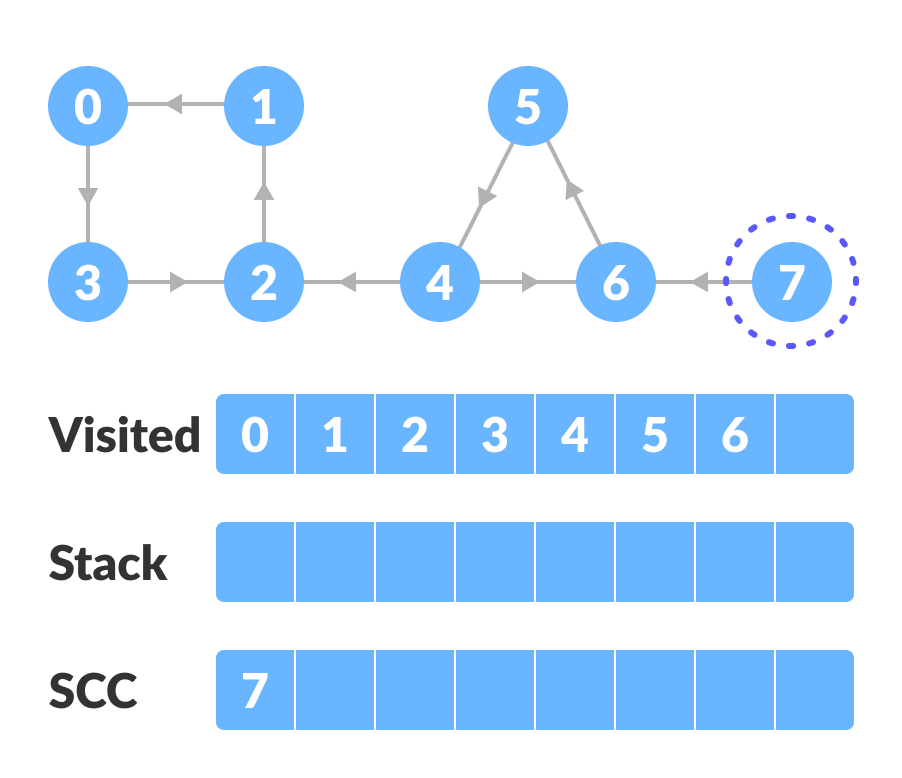强连通分量

因此，强连通分量是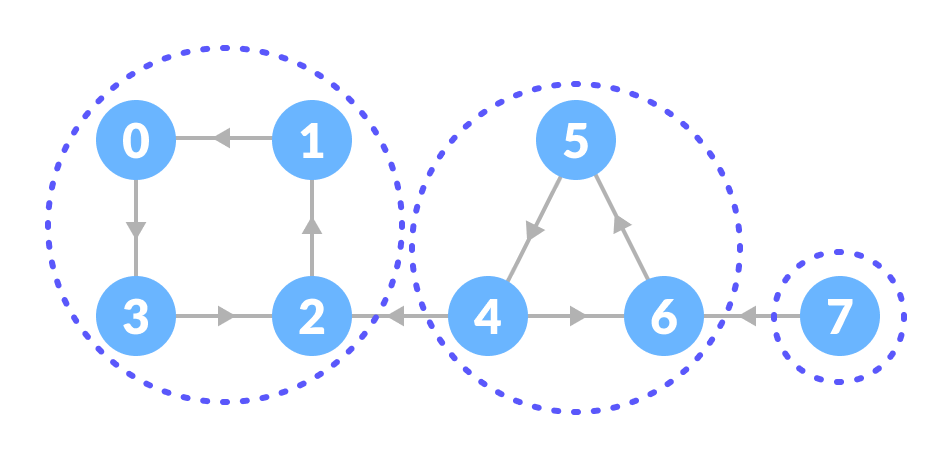： | | | —- | | 所有强连通分量 |

Kosaraju 的复杂性

Kosaraju 的算法在线性时间内运行，即O(V+E)。

强连接组件的应用

车辆路径应用
地图
形式验证中的模型检查

Kosaraju 的实现

// Kosaraju's algorithm to find strongly connected components in Java
import java.util.*;
import java.util.LinkedList;
class Graph {
    private int V;
    private LinkedList<Integer> adj[];
    // Create a graph
    Graph(int s) {
        V = s;
        adj = new LinkedList[s];
        for (int i = 0; i < s; ++i)
            adj[i] = new LinkedList();
    }
  // Add edge
    void addEdge(int s, int d) {
        adj[s].add(d);
    }
    // DFS
    void DFSUtil(int s, boolean visitedVertices[]) {
        visitedVertices[s] = true;
        System.out.print(s + " ");
        int n;
        Iterator<Integer> i = adj[s].iterator();
        while (i.hasNext()) {
            n = i.next();
            if (!visitedVertices[n])
                DFSUtil(n, visitedVertices);
        }
    }
    // Transpose the graph
    Graph Transpose() {
        Graph g = new Graph(V);
        for (int s = 0; s < V; s++) {
            Iterator<Integer> i = adj[s].listIterator();
            while (i.hasNext())
                g.adj[i.next()].add(s);
        }
        return g;
    }
    void fillOrder(int s, boolean visitedVertices[], Stack stack) {
        visitedVertices[s] = true;
        Iterator<Integer> i = adj[s].iterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visitedVertices[n])
                fillOrder(n, visitedVertices, stack);
        }
        stack.push(new Integer(s));
    }
    // Print strongly connected component
    void printSCC() {
        Stack stack = new Stack();
        boolean visitedVertices[] = new boolean[V];
        for (int i = 0; i < V; i++)
            visitedVertices[i] = false;
        for (int i = 0; i < V; i++)
            if (visitedVertices[i] == false)
                fillOrder(i, visitedVertices, stack);
        Graph gr = Transpose();
        for (int i = 0; i < V; i++)
            visitedVertices[i] = false;
        while (stack.empty() == false) {
            int s = (int) stack.pop();
            if (visitedVertices[s] == false) {
                gr.DFSUtil(s, visitedVertices);
                System.out.println();
            }
        }
    }
    public static void main(String args[]) {
        Graph g = new Graph(8);
        g.addEdge(0, 1);
        g.addEdge(1, 2);
        g.addEdge(2, 3);
        g.addEdge(2, 4);
        g.addEdge(3, 0);
        g.addEdge(4, 5);
        g.addEdge(5, 6);
        g.addEdge(6, 4);
        g.addEdge(6, 7);
        System.out.println("Strongly Connected Components:");
        g.printSCC();
    }
}