梯度下降

1.什么是梯度下降？

比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。从上面的解释可以看出，梯度下降不一定能够找到全局的最优解，有可能是一个局部最优解。当然，如果损失函数是凸函数，梯度下降法得到的解就一定是全局最优解。

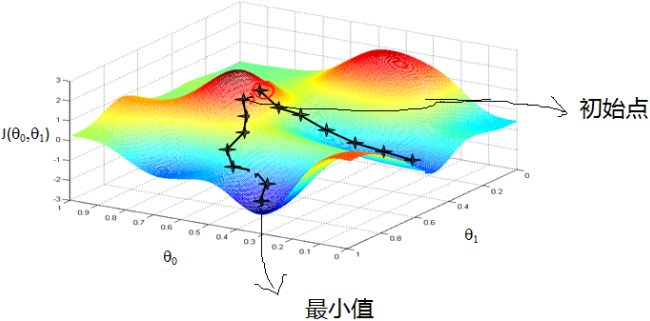
2.梯度下降的实现

梯度下降和下山的场景类似，首先我们有一个函数，这个函数类比于山，我们的目标是找到函数的最小值，也就是山底。根据之前的理论，那么我们要走的就是找到最快的下山方式，也就是最陡峭的地方。对应到函数中，就是找到函数值下降最快的地方，也就是梯度的反方向（梯度的正方向为函数值上升最快的地方）。在函数中，梯度就是对函数求微分。
(1)对于单变量函数,以下是求微分的实例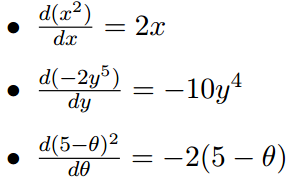

(2)对于多变量函数,求微分是分别对每个变量进行求微分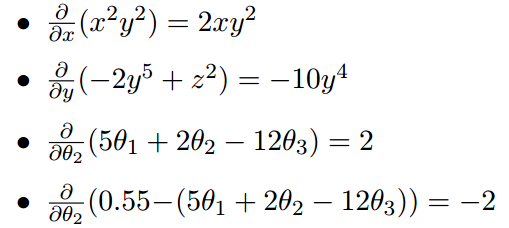

梯度实际上就是多变量微分的一般化。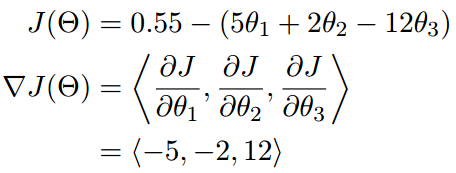

可以看到梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>表示，说明梯度其实是一个向量。
(1)在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
(2)在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向
这也就说明了为什么我们需要千方百计的求取梯度：我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。

下面从数学上解释梯度下降算法的计算过程和思想。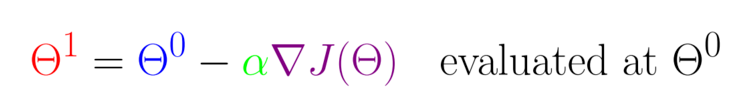

此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反方向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ这个点。这里关键是对步长α的理解，α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大扯着蛋，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。有了以上的知识储备，我们就可以看几个梯度下降算法的小实例，首先从单变量的函数开始。梯度下降的计算公式


我们开始进行梯度下降的迭代计算过程：

经过四次运算，就基本到达了函数的最低点，也就是山底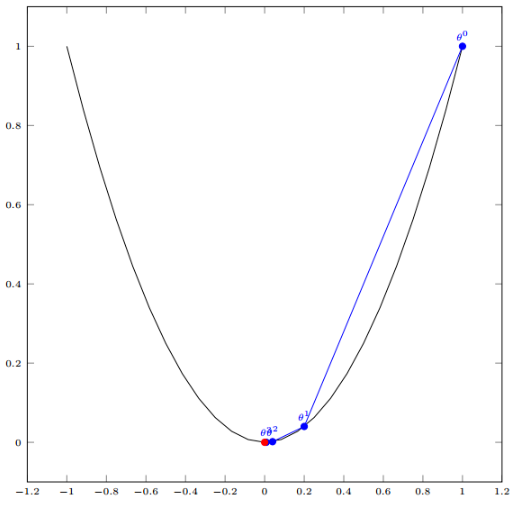

多函数梯度下降：
假设目标函数是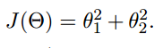

假设起点为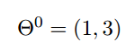

初始的学习率为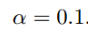

函数的梯度为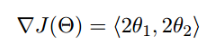

进行多次迭代

这个时候，基本接近函数的最小值点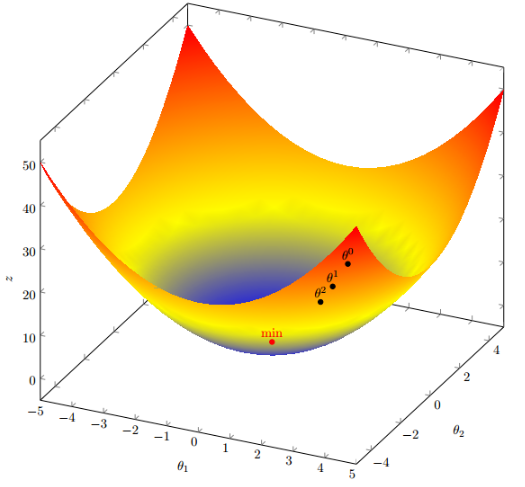

3.梯度下降用于拟合线性回归

下图是一个线性回归的例子，假设现在我们有一系列的点，如下图所示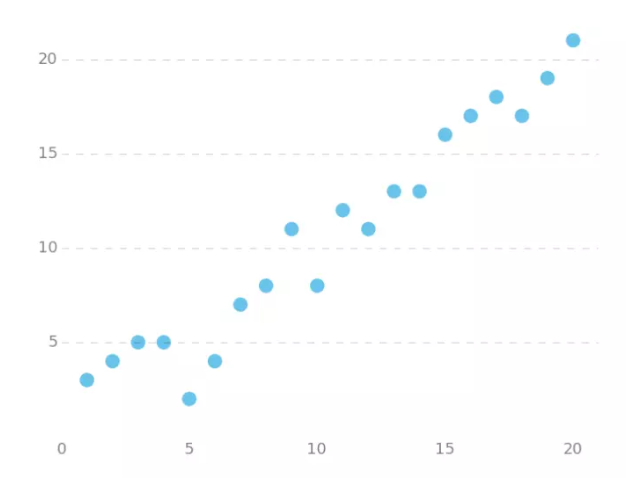

我们将用梯度下降法拟合出这条直线。首先，我们需要定义一个代价函数，代价函数是干什么的？是用来反映预测值和真实值之间差距问题的，对于点x，假设预测值用h(x)来表示，点x对应的真实值为y，那么预测值和真实值之间的差距可以表示为|h(x)-y|，假设图中共有m个点，那么总差距可以表示为，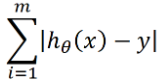

平均代价可以表示为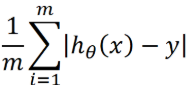

在这里我们并不是要求出预测值和真实值之间具体的数值是多少，想想定义误差函数是为了什么？带绝对值的代价函数是我们自己定义的，它只是所有误差函数中的一种，是用来表示一个点的真实值和预测值之间的差值，我们用这个差值来表示代价函数，那差值的一半我们定义为代价函数可不可以，当然可以。平方可以吗，也是可以的。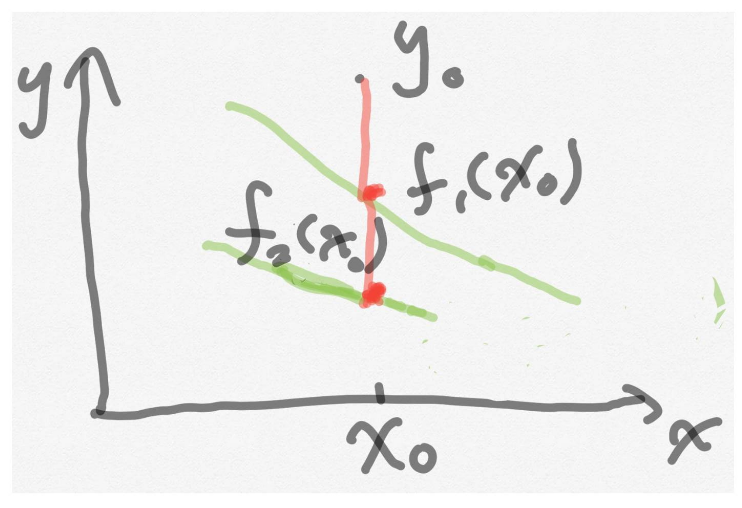

我们的目标是看这两条直线哪一个拟合得更好，由于评价规则对两条直线f(x)和f(x)是一样的，因此可以将绝对值转化为平方。代价函数(cost function)有五种，最常用的是均方误差代价函数，它可以写成如下形式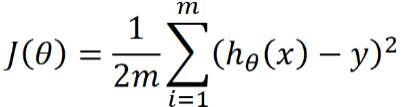

此公示中
（1）m是数据集中点的个数
（2）½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
（3）x、y 是数据集中每个点的真实x、y坐标的值，注意它们不是变量而是常量。
（4）h 是我们的预测函数，根据每一个输入x，根据h计算得到预测的y值，即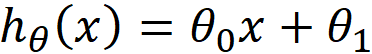

代价函数中的变量有两个：θ和θ，所以是一个多变量的梯度下降问题，求解出代价函数的梯度，也就是分别对两个变量进行微分。在对函数进行微分处理之前，首先搞清楚以下几点
（1）前面不是提出了线性回归吗？线性体现在哪里？
答 ：线性体现在训练函数上，正是因为它是线性的，我们才可以写成如下的形式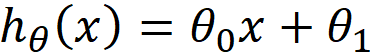

这里要解决的其实就是求出θ和θ
（2）这里的代价函数作用是什么？
答：我们可以拟合出多条直线h（x），但是它们的拟合程度有好有坏，代价函数就是来评判好坏的。
（3）梯度下降在这里的作用是什么？
答：帮助我们找到最好的拟合直线，前面已经提到过，梯度的方向就是求函数最小值的方向。

我们如果把代价函数看作是我们处在山上的某个点，那么我们要做的就是找到这座山的最低点，沿着梯度的反方向就是它下降最快的地方。为什么要求下降最快的方向呢？关于这个问题目前还没有找到最确切的说法，以下是我自己思考的两个理由
（1）为什么要用梯度下降？因为方便，求导数然后取这个导数的负值就是梯度下降的方向。试想，我们如果来找一个沿着其他方向下降的，它有明确的公式吗？没有。梯度下降不仅下降最快还有明确的公式!!
（2）速度快，这点是非常重要的。再把求代价函数的最小值看作是一个下山的过程，那么这个下降的过程速度快慢有两个决定因素，第一是步长，第二是下降的方向，越快找到这个解越好，减少存储中间结果的内存。此外，下降的方向如果是最快的方向，那么对步长来说就有调整的空间了，因为如果下降的速度很慢，那么为了能尽快找到这个最小值，可能会采用较大的步长α，这样可能会错失最小值点。（下图选自Andrew NG 博客贴图）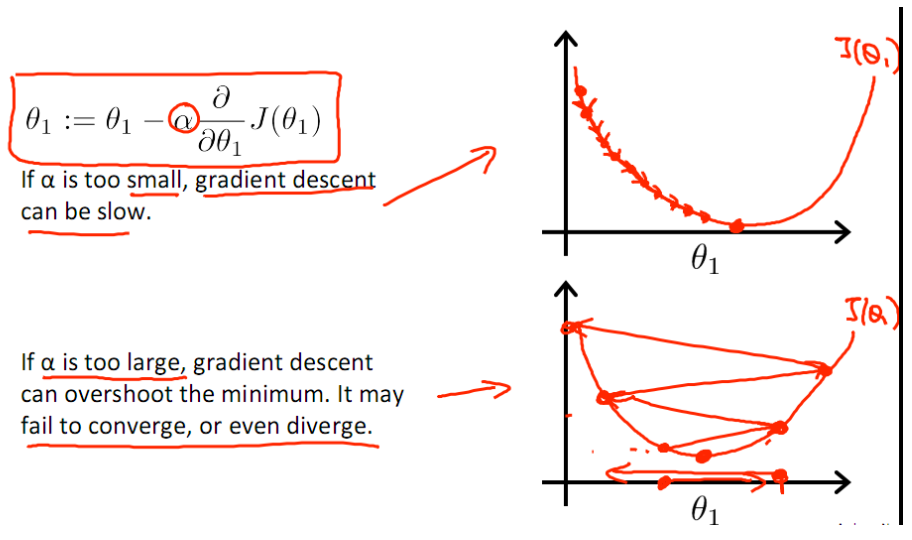

算法过程：
（1）算法相关参数初始化：主要是初始化终止距离ε以及步长α，在没有任何先验知识的时候，将步长初始化为1。在调优的时候再优化。
（2）确定当前位置的损失函数的梯度，对于θ,其梯度表达式如下：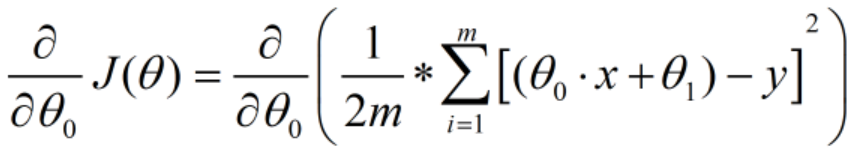

（3）用步长乘以损失函数的梯度，得到当前位置下降的距离，即

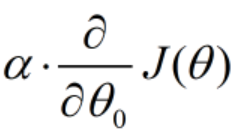
（4）同理对θ求梯度，并求出当前位置下降的距离
（5）确定是否θ和θ的下降距离都小于初始化终止距离ε（这个值通常很小，说明这个时候已经下降不动多少了），如果都小于的话，则算法终止并且θ和θ即为最终结果；如果不是都小于初始化终止距离，进入下一步。
（6）更新θ和θ，此时它们的表达式为

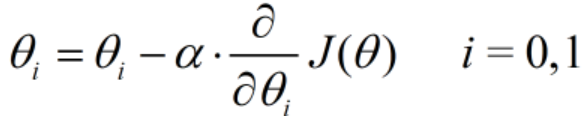
（7）转入步骤2~5，看看这次是否两个参数θ和θ都小于初始化终止距离ε

4.代码实现

最后是coding time，前面已经将代价函数J(θ)表示为

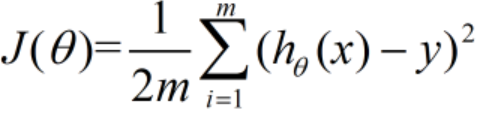
h(x)由于是线性函数，它的一般表达式为：

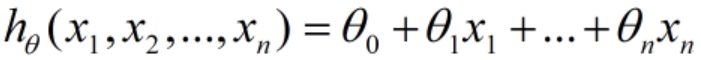
假设函数的矩阵表达式为h(X)=Xθ，其中，h(X)为m1的向量，θ为(n+1)1的向量，里面有n+1个代数法的模型参数。X为m(n+1)维的矩阵，m代表样本的个数，n+1代表样本的特征数。这样损失函数就可以表达为：

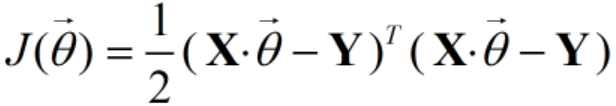
其中Y是样本的输出向量，维度为m1.对J(θ)求偏导就有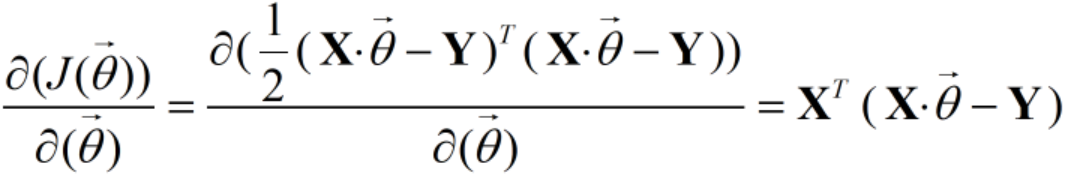

PS：关于损失函数以及损失函数求偏导这个公式比较复杂，后面有时间在来研究
PPS：博客[1]和博客[2]在损失函数和损失函数求偏导这个地方有所出入，本文公式部分参照博客[2]，代码部分参照博客[1]

# -*- coding: utf-8 -*-
"""
@author: Haojie Shu
@time: 2019/03/18
@description:梯度下降函数来拟合线性回归
"""
import numpy as np
m = 20
X0 = np.ones((m, 1))  # 创造全1数组,括号里的参数是shape,表示m行1列
# np.arrange:创造等差数列,包含三个参数,第一个参数是起始值,第二个参数是步长,默认为1, 最后一个是终止值,左闭右开
# np.reshape:对数列进行转置,它的标准形式是np.reshape(array, newshape),但是也可以像本例这样直接写成np.arrange.reshape
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))  # hstack将两个列向量合并,vstack表示两个行向量合并
y = np.array([3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12, 11, 13, 13, 16, 17, 18, 17, 19, 21]).reshape(m, 1)
alpha = 0.01  # alpha表示步长
def error_function(theta, X, y):
    """
    定义代价函数,差值的平方
    """
    diff = np.dot(X, theta) - y  # np.dot 两个向量的乘法
    # np.transpose 对数组进行转置
    return (1./2/m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
    """
    代价函数的梯度
    """
    diff = np.dot(X, theta) - y
    return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
    """
    梯度下降迭代计算
    """
    theta = np.array([1, 1]).reshape(2, 1)  # 初始出发点
    gradient = gradient_function(theta, X, y)  # 在初始出发点这个地方求偏导
    while not np.all(np.absolute(gradient) <= 1e-5):  # np.all,判断是否所有的数组元素都为True
        theta = theta - alpha * gradient  # 第一趟:while语句不满足,theta的值发生改变
        gradient = gradient_function(theta, X, y)  # 同样gradient的值也要改变,继续判断while语句是否满足
    return theta
optimal = gradient_descent(X, y, alpha)  # 满足条件时的theta的值
print('optimal:', optimal)
print('error function:', error_function(optimal, X, y)[0, 0])  # 代价函数的值,即用这个直线拟合,一共产生了多少误差

整理来自
1.《深入浅出—梯度下降法及其实现》https://www.jianshu.com/p/c7e642877b0e
2.《梯度下降（Gradient Descent）小结》https://www.cnblogs.com/pinard/p/5970503.html

5.后续

关于梯度下降，在前面其实花了很多的时间来了解前面的问题，即“为什么要用梯度下降来求损失函数的最小值？”，这个问题有一定的价值，但是没必要过分纠结。这里需要注意的是，由于梯度下降的计算量较大，所以它在实际算法中的应用是较少的，这里只需要搞清楚它的原理即可。后面重点了解梯度下降算法的升级版，随机梯度下降（Stochastic Gradient Descent,SGD）。