开篇问题

淘宝的“双十一”购物节有各种促销活动，比如“满 200 元减 50 元”。假设你女朋友的购物车中有 n 个（n>100）想买的商品，她希望从里面选几个，在凑够满减条件的前提下，让选出来的商品价格总和最大程度地接近满减条件（200 元），这样就可以极大限度地“薅羊毛”。如何用代码来搞定呢?
动态规划。

动态规划学习路线

动态规划比较适合用来求解最优问题，比如求最大值、最小值等等。
它可以非常显著地降低时间复杂度，提高代码的执行效率。不过，它也是出了名的难学。它的主要学习难点跟递归类似，那就是，求解问题的过程不太符合人类常规的思维方式。对于新手来说，要想入门确实不容易。不过，等你掌握了之后，你会发现，实际上并没有想象中那么难。
为了更容易理解动态规划，分了三节来讲解。这三节分别是，初识动态规划、动态规划理论、动态规划实战。
第一节，通过两个非常经典的动态规划问题模型，展示我们为什么需要动态规划，以及动态规划解题方法是如何演化出来的。实际上，你只要掌握了这两个例子的解决思路，对于其他很多动态规划问题，你都可以套用类似的思路来解决。
第二节，总结动态规划适合解决的问题的特征，以及动态规划解题思路。除此之外，将贪心、分治、回溯、动态规划这四种算法思想放在一起，对比分析它们各自的特点以及适用的场景。
第三节，应用第二节讲的动态规划理论知识，实战解决三个非常经典的动态规划问题，加深你对理论的理解。弄懂了这三节中的例子，对于动态规划这个知识点，你就算是入门了。

0-1背包问题

贪心 回溯算法时，也多次讲到背包问题。依然用背包来举例。
对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制的前提下，背包中物品总重量的最大值是多少呢？
之前说过可以用回溯的解决方法，也就是穷举搜索所有可能的装法，然后找出满足条件的最大值。不过，回溯算法的复杂度比较高，是指数级别的。那有没有什么规律，可以有效降低时间复杂度呢？

  2. // 回溯算法实现。注意：我把输入的变量都定义成了成员变量。
  3. private int maxW = Integer.MIN_VALUE; // 结果放到maxW中
  4. private int[] weight = {2，2，4，6，3};  // 物品重量
  5. private int n = 5; // 物品个数
  6. private int w = 9; // 背包承受的最大重量
  7. public void f(int i, int cw) { // 调用f(0, 0)
  8.   if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了
  9.     if (cw > maxW) maxW = cw;
  10.     return;
  11.   }
  12.   f(i+1, cw); // 选择不装第i个物品
  13.   if (cw + weight[i] <= w) {
  14.     f(i+1,cw + weight[i]); // 选择装第i个物品
  15.   }
  16. }

对于f(i+1,cw)和 之后的if
理解是两个同时展开 对于当前的f 分出了两个部分 一个是不装物品的f(i+1,cw) 另一个是装物品的f(i+1,cw+weight[i]) （但需要判断装进去是否超重）。
假设背包最大重量9，有5个不同物品，每个物品重量是2，2，4，6，3. 如果用回溯求解，用递归树画出来，如下。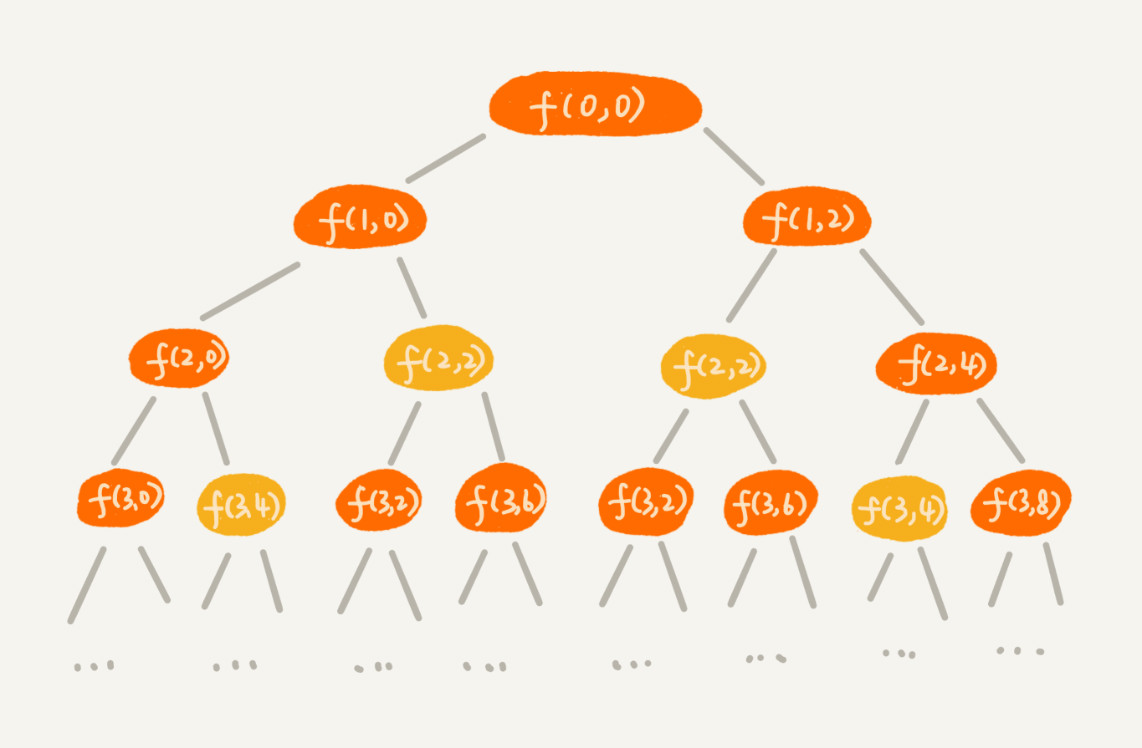
40|初识动态规划：如何巧妙解决“双十一”购物时的凑单问题？ - 图1

递归树中的每个节点表示一种状态，我们用（i, cw）来表示。其中，i 表示将要决策第几个物品是否装入背包，cw 表示当前背包中物品的总重量。比如，（2，2）表示我们将要决策第 2 个物品是否装入背包，在决策前，背包中物品的总重量是 2。
每个f(i,cw)都是一个状态。所以，不管之前走的具体路径是否一样，但只要i和cw相同，说明当前所处的状态是一样的。而本问题是要求最终的最大重量，所以如果i和cw相同，那之前肯定计算过了，也就不用再做重复的工作了。
从递归树中，你应该能会发现，有些子问题的求解是重复的，比如图中 f(2, 2) 和 f(3,4) 都被重复计算了两次。我们可以借助递归那一节讲的“备忘录”的解决方式，记录已经计算好的 f(i, cw)，当再次计算到重复的 f(i, cw) 的时候，可以直接从备忘录中取出来用，就不用再递归计算了，这样就可以避免冗余计算。
递归的优化思路就是加一个备忘录 如果计算到重复的状态的时候，可以直接从备忘录中取出来用， 就不用再递归计算了,避免冗余计算。

  2. private int maxW = Integer.MIN_VALUE; // 结果放到maxW中
  3. private int[] weight = {2，2，4，6，3};  // 物品重量
  4. private int n = 5; // 物品个数
  5. private int w = 9; // 背包承受的最大重量
  6. private boolean[][] mem = new boolean[5][10]; // 备忘录，默认值false
  7. public void f(int i, int cw) { // 调用f(0, 0)
  8.   if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了
  9.     if (cw > maxW) maxW = cw;
  10.     return;
  11.   }
  12.   if (mem[i][cw]) return; // 重复状态
  13.   mem[i][cw] = true; // 记录(i, cw)这个状态
  14.   f(i+1, cw); // 选择不装第i个物品
  15.   if (cw + weight[i] <= w) {
  16.     f(i+1,cw + weight[i]); // 选择装第i个物品
  17.   }
  18. }

该解决方法。实际上，跟动态规划的执行效率没什么差别了。
但下面还看一下动态规划如何处理。
我们把整个求解过程分为 n 个阶段，每个阶段会决策一个物品是否放到背包中。每个物品决策（放入或者不放入背包）完之后，背包中的物品的重量会有多种情况，也就是说，会达到多种不同的状态，对应到递归树中，就是有很多不同的节点。
我们把每一层重复的状态（节点）合并，只记录不同的状态，然后基于上一层的状态集合，来推导下一层的状态集合。我们可以通过合并每一层重复的状态，这样就保证每一层不同状态的个数都不会超过 w 个（w 表示背包的承载重量），也就是例子中的 9。于是，我们就成功避免了每层状态个数的指数级增长。（因为合并了重复的重量状态，所以最多重量情况就是10 0，1，2，3，4，5，6，7，8，9）.
用二维数组 states[n][w+1]来记录每层可以达到的不同状态。
第 0 个（下标从 0 开始编号）物品的重量是 2，要么装入背包，要么不装入背包，决策完之后，会对应背包的两种状态，背包中物品的总重量是 0 或者 2。我们用 states[0][0]=true 和 states[0][2]=true 来表示这两种状态。
第 1 个物品的重量也是 2，基于之前的背包状态，在这个物品决策完之后，不同的状态有 3 个，背包中物品总重量分别是 0(0+0)，2(0+2 or 2+0)，4(2+2)。我们用 states[1][0]=true，states[1][2]=true，states[1][4]=true 来表示这三种状态。
以此类推，直到考察完所有的物品后，整个 states 状态数组就都计算好了。我把整个计算的过程画了出来，你可以看看。图中 0 表示 false，1 表示 true。我们只需要在最后一层，找一个值为 true 的最接近 w（这里是 9）的值，就是背包中物品总重量的最大值。

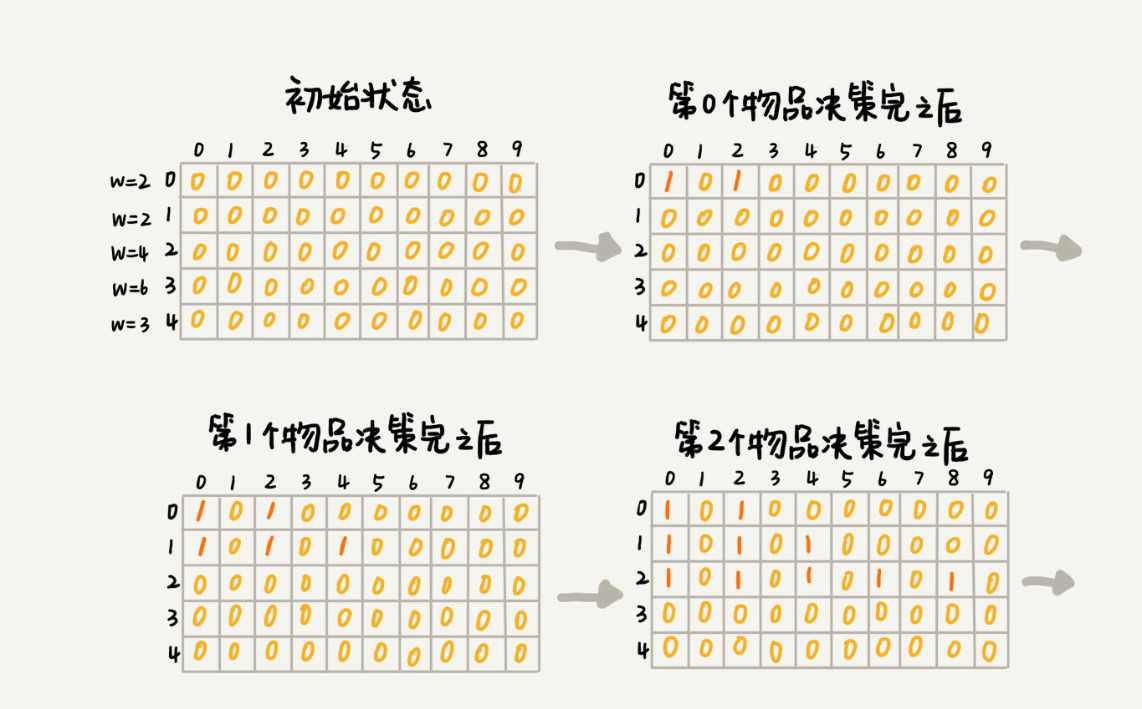
40|初识动态规划：如何巧妙解决“双十一”购物时的凑单问题？ - 图2

行：第x个物品决策完后情况。
列：重量的可能。

  2. weight:物品重量，n:物品个数，w:背包可承载重量
  3. public int knapsack(int[] weight, int n, int w) {
  4.   boolean[][] states = new boolean[n][w+1]; // 默认值false
  5.   states[0][0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
  6.   if (weight[0] <= w) {
  7.     states[0][weight[0]] = true;//第一行赋初值，初始化
  8.   }
  9.   for (int i = 1; i < n; ++i) { // 动态规划状态转移 最优解和取物品的顺序无关，是个组合问题，所以可以从第一个开始，逐个考察放与不放的，就可以覆盖所有情况。 一个个取物品，也是一步步的状态转移
  10.     for (int j = 0; j <= w; ++j) {// 不把第i个物品放入背包
  11.       if (states[i-1][j] == true) states[i][j] = states[i-1][j];
  12.     }
  13.     for (int j = 0; j <= w-weight[i]; ++j) {//把第i个物品放入背包
  14.       if (states[i-1][j]==true) states[i][j+weight[i]] = true;
  15.     }
  16.   }
  17.   for (int i = w; i >= 0; --i) { // 输出结果
  18.     if (states[n-1][i] == true) return i;
  19.   }
  20.   return 0;
  21. }

第9行 最优解和取物品的顺序无关，是个组合问题，所以可以从第一个开始，逐个考察放与不放的，就可以覆盖所有情况。 一个个取物品，也是一步步的状态转移
第11行 这里states[i-1][j] == true是上一层的放置状态，把上一层的状态赋值给当前层，即：没有放入背包，且上一层的背包状态有效 为true，将上层的状态要拷贝到当前层。
第13行：这里其实比较难理解。w - weight[i] 为减去当前 i 项物品重量后，剩余的重量，通过for循环遍历，判断上一层 i - 1 的状态中是否有满足的解，states[i - 1][j] == true。如果有满足解，加入到第 i 层的状态中，j + weight[i]。
第18行：所有决策都走完，所以只需要遍历第n-1层，从右往左找到最大可能的那个状态
实际上，这就是一种用动态规划解决问题的思路。我们把问题分解为多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。这也是动态规划这个名字的由来，你可以自己体会一下，是不是还挺形象的？
妙。首先，可以分解为多阶段，其次，当前阶段可以利用上一个阶段来获取。这是动态规划的关键。如果当前阶段和历史状态关联太多，就没法动态规划了。如果当前i和i-1，i-2这种关联是不是也可以。那就是必须是有限的状态关联，才能动态规划。
前面我们讲到，用回溯算法解决这个问题的时间复杂度 O(2^n)，是指数级的。那动态规划解决方案的时间复杂度是多少呢？分析一下。
这个代码的时间复杂度非常好分析，耗时最多的部分就是代码中的两层 for 循环，所以时间复杂度是 O(nw)。n 表示物品个数，w 表示背包可以承载的总重量。
从理论上讲，指数级的时间复杂度肯定要比 O(nw) 高很多，但是为了让你有更加深刻的感受，我来举一个例子给你比较一下。
假设有 10000 个物品，重量分布在 1 到 15000 之间，背包可以承载的总重量是 30000。如果我们用回溯算法解决，用具体的数值表示出时间复杂度，就是 2^10000，这是一个相当大的一个数字。如果我们用动态规划解决，用具体的数值表示出时间复杂度，就是 10000*30000。虽然看起来也很大，但是和 2^10000 比起来，要小太多了。
尽管动态规划的执行效率比较高，但是就刚刚的代码实现来说，我们需要额外申请一个 n 乘以 w+1 的二维数组，对空间的消耗比较多。所以，有时候，我们会说，动态规划是一种空间换时间的解决思路。你可能要问了，有什么办法可以降低空间消耗吗？
实际上，我们只需要一个大小为 w+1 的一维数组就可以解决这个问题。动态规划状态转移的过程，都可以基于这个一维数组来操作。

  2. public static int knapsack2(int[] items, int n, int w) {
  3.   boolean[] states = new boolean[w+1]; // 默认值false
  4.   states[0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
  5.   if (items[0] <= w) {
  6.     states[items[0]] = true;
  7.   }
  8.   for (int i = 1; i < n; ++i) { // 动态规划
  9.     for (int j = w-items[i]; j >= 0; --j) {//把第i个物品放入背包
  10.       if (states[j]==true) states[j+items[i]] = true;
  11.     }
  12.   }
  13.   for (int i = w; i >= 0; --i) { // 输出结果
  14.     if (states[i] == true) return i;
  15.   }
  16.   return 0;
  17. }

state[j] 表示能否达到j的重量。
第8行：j需要从大到小来处理，如果从小到大，会出现for循环重复计算问题。
由于使用的一维数组，无法获得上一个状态（i - 1）的可达性；这时候如果从前往后，后面的结果，会用到前面错误的结果（相当于多放了，并不是 i 和 i - 1 之间的状态转移）。
由于动态规划的特点，某个状态是基于其前一个状态得来的，因此需要去判断前一个状态是否可达。而j是从大到小还是从小到大处理？还是需要看具体问题，这里的问题场景是重量的累加，也就是说我们需要把状态的值从小到大累加列举出来，如果我们需要找某个状态值的前一个状态，那前一个状态势必比当前状态小，所以这里代表状态值的j就得从大往小去找前一个可达的状态。

0-1 背包问题升级版

刚刚讲背包问题，只涉及背包重量和物品重量。现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品，我们选择将某些物品装入背包，在满足背包最大重量限制的前提下，背包中可装入物品的总价值最大是多少呢？
这个问题依旧可以用回溯算法来解决。

  2. private int maxV = Integer.MIN_VALUE; // 结果放到maxV中
  3. private int[] items = {2，2，4，6，3};  // 物品的重量
  4. private int[] value = {3，4，8，9，6}; // 物品的价值
  5. private int n = 5; // 物品个数
  6. private int w = 9; // 背包承受的最大重量
  7. public void f(int i, int cw, int cv) { // 调用f(0, 0, 0)
  8.   if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了
  9.     if (cv > maxV) maxV = cv;
  10.     return;
  11.   }
  12.   f(i+1, cw, cv); // 选择不装第i个物品
  13.   if (cw + weight[i] <= w) {
  14.     f(i+1,cw+weight[i], cv+value[i]); // 选择装第i个物品
  15.   }
  16. }

针对上面的代码，我们还是照例画出递归树。在递归树中，每个节点表示一个状态。现在我们需要 3 个变量（i, cw, cv）来表示一个状态。其中，i 表示即将要决策第 i 个物品是否装入背包，cw 表示当前背包中物品的总重量，cv 表示当前背包中物品的总价值。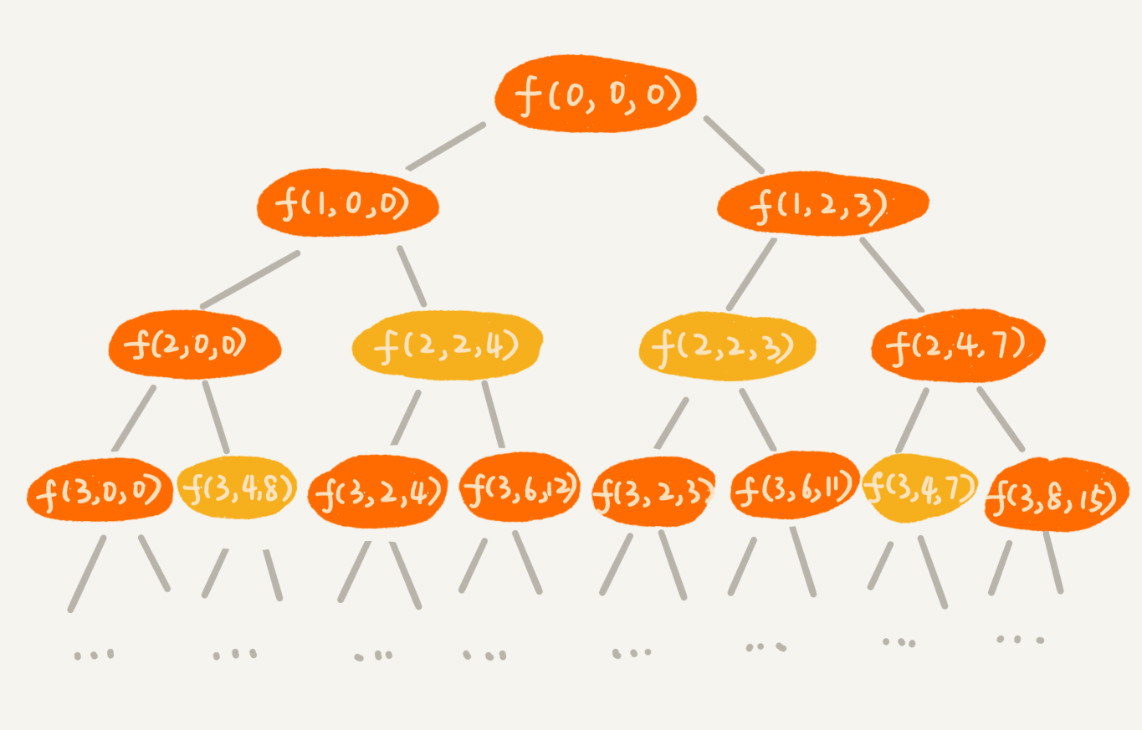
40|初识动态规划：如何巧妙解决“双十一”购物时的凑单问题？ - 图3
我们发现，在递归树中，有几个节点的 i 和 cw 是完全相同的，比如 f(2,2,4) 和 f(2,2,3)。在背包中物品总重量一样的情况下，f(2,2,4) 这种状态对应的物品总价值更大，我们可以舍弃 f(2,2,3) 这种状态，只需要沿着 f(2,2,4) 这条决策路线继续往下决策就可以。
也就是说，对于 (i, cw) 相同的不同状态，那我们只需要保留 cv 值最大的那个，继续递归处理，其他状态不予考虑。
思路说完了，但是代码如何实现呢？如果用回溯算法，这个问题就没法再用“备忘录”解决了。所以，我们就需要换一种思路，看看动态规划是不是更容易解决这个问题？
我们还是把整个求解过程分为 n 个阶段，每个阶段会决策一个物品是否放到背包中。每个阶段决策完之后，背包中的物品的总重量以及总价值，会有多种情况，也就是会达到多种不同的状态。
我们用一个二维数组 states[n][w+1]，来记录每层可以达到的不同状态。不过这里数组存储的值不再是 boolean 类型的了，而是当前状态对应的最大总价值。我们把每一层中 (i, cw) 重复的状态（节点）合并，只记录 cv 值最大的那个状态，然后基于这些状态来推导下一层的状态。
代码如下

  2. public static int knapsack3(int[] weight, int[] value, int n, int w) {
  3.   int[][] states = new int[n][w+1];
  4.   for (int i = 0; i < n; ++i) { // 初始化states
  5.     for (int j = 0; j < w+1; ++j) {
  6.       states[i][j] = -1;
  7.     }
  8.   }
  9.   states[0][0] = 0;
  10.   if (weight[0] <= w) {
  11.     states[0][weight[0]] = value[0];
  12.   }
  13.   for (int i = 1; i < n; ++i) { //动态规划，状态转移
  14.     for (int j = 0; j <= w; ++j) { // 不选择第i个物品
  15.       if (states[i-1][j] >= 0) states[i][j] = states[i-1][j];
  16.     }
  17.     for (int j = 0; j <= w-weight[i]; ++j) { // 选择第i个物品
  18.       if (states[i-1][j] >= 0) {
  19.         int v = states[i-1][j] + value[i];
  20.         if (v > states[i][j+weight[i]]) {
  21.           states[i][j+weight[i]] = v;
  22.         }
  23.       }
  24.     }
  25.   }
  26.   // 找出最大值
  27.   int maxvalue = -1;
  28.   for (int j = 0; j <= w; ++j) {
  29.     if (states[n-1][j] > maxvalue) maxvalue = states[n-1][j];
  30.   }
  31.   return maxvalue;
  32. }

时间复杂度是 O(nw)，空间复杂度也是 O(nw)。

解答开篇

对于这个问题，你当然可以利用回溯算法，穷举所有的排列组合，看大于等于 200 并且最接近 200 的组合是哪一个？但是，这样效率太低了点，时间复杂度非常高，是指数级的。当 n 很大的时候，可能“双十一”已经结束了，你的代码还没有运行出结果，这显然会让你在女朋友心中的形象大大减分。
实际上，它跟第一个例子中讲的 0-1 背包问题很像，只不过是把“重量”换成了“价格”而已。购物车中有 n 个商品。我们针对每个商品都决策是否购买。每次决策之后，对应不同的状态集合。我们还是用一个二维数组 states[n][x]，来记录每次决策之后所有可达的状态。不过，这里的 x 值是多少呢？
0-1 背包问题中，我们找的是小于等于 w 的最大值，x 就是背包的最大承载重量 w+1。对于这个问题来说，我们要找的是大于等于 200（满减条件）的值中最小的，所以就不能设置为 200 加 1 了。就这个实际的问题而言，如果要购买的物品的总价格超过 200 太多，比如 1000，那这个羊毛“薅”得就没有太大意义了。所以，我们可以限定 x 值为 1001。
不过，这个问题不仅要求大于等于 200 的总价格中的最小的，我们还要找出这个最小总价格对应都要购买哪些商品。实际上，我们可以利用 states 数组，倒推出这个被选择的商品序列。我先把代码写出来，待会再照着代码给你解释。

  2. // items商品价格，n商品个数, w表示满减条件，比如200
  3. public static void double11advance(int[] items, int n, int w) {
  4.   boolean[][] states = new boolean[n][3*w+1];//超过3倍就没有薅羊毛的价值了
  5.   states[0][0] = true;  // 第一行的数据要特殊处理
  6.   if (items[0] <= 3*w) {
  7.     states[0][items[0]] = true;
  8.   }
  9.   for (int i = 1; i < n; ++i) { // 动态规划
  10.     for (int j = 0; j <= 3*w; ++j) {// 不购买第i个商品
  11.       if (states[i-1][j] == true) states[i][j] = states[i-1][j];
  12.     }
  13.     for (int j = 0; j <= 3*w-items[i]; ++j) {//购买第i个商品
  14.       if (states[i-1][j]==true) states[i][j+items[i]] = true;
  15.     }
  16.   }
  18.   int j;
  19.   for (j = w; j < 3*w+1; ++j) { 
  20.     if (states[n-1][j] == true) break; // 输出结果大于等于w的最小值
  21.   }
  22.   if (j == 3*w+1) return; // 没有可行解
  23.   for (int i = n-1; i >= 1; --i) { // i表示二维数组中的行，j表示列
  24.     if(j-items[i] >= 0 && states[i-1][j-items[i]] == true) {
  25.       System.out.print(items[i] + " "); // 购买这个商品
  26.       j = j - items[i];
  27.     } // else 没有购买这个商品，j不变。
  28.   }
  29.   if (j != 0) System.out.print(items[0]);
  30. }

代码的前半部分跟 0-1 背包问题没有什么不同，我们着重看后半部分，看它是如何打印出选择购买哪些商品的。
状态 (i, j) 只有可能从 (i-1, j) 或者 (i-1, j-value[i]) 两个状态推导过来。所以，我们就检查这两个状态是否是可达的，也就是 states[i-1][j]或者 states[i-1][j-value[i]]是否是 true。（表格中一个true的位置可能是由它上一行的true这轮不选推导过来，或者是上一行放弃了第i个物品过来）
如果 states[i-1][j]可达，就说明我们没有选择购买第 i 个商品，如果 states[i-1][j-value[i]]可达，那就说明我们选择了购买第 i 个商品。我们从中选择一个可达的状态（如果两个都可达，就随意选择一个），然后，继续迭代地考察其他商品是否有选择购买。

内容小结

天的内容不涉及动态规划的理论，我通过两个例子，给你展示了动态规划是如何解决问题的，并且一点一点详细给你讲解了动态规划解决问题的思路。这两个例子都是非常经典的动态规划问题，只要你真正搞懂这两个问题，基本上动态规划已经入门一半了。所以，你要多花点时间，真正弄懂这两个问题。
从例子中，你应该能发现，大部分动态规划能解决的问题，都可以通过回溯算法来解决，只不过回溯算法解决起来效率比较低，时间复杂度是指数级的。动态规划算法，在执行效率方面，要高很多。尽管执行效率提高了，但是动态规划的空间复杂度也提高了，所以，很多时候，我们会说，动态规划是一种空间换时间的算法思想。
我前面也说了，今天的内容并不涉及理论的知识。这两个例子的分析过程，我并没有涉及任何高深的理论方面的东西。而且，我个人觉得，贪心、分治、回溯、动态规划，这四个算法思想有关的理论知识，大部分都是“后验性”的，也就是说，在解决问题的过程中，我们往往是先想到如何用某个算法思想解决问题，然后才用算法理论知识，去验证这个算法思想解决问题的正确性。所以，你大可不必过于急于寻求动态规划的理论知识。

课后思考

“杨辉三角”
杨辉三角”不知道你听说过吗？我们现在对它进行一些改造。每个位置的数字可以随意填写，经过某个数字只能到达下面一层相邻的两个数字。
假设你站在第一层，往下移动，我们把移动到最底层所经过的所有数字之和，定义为路径的长度。请你编程求出从最高层移动到最底层的最短路径长度。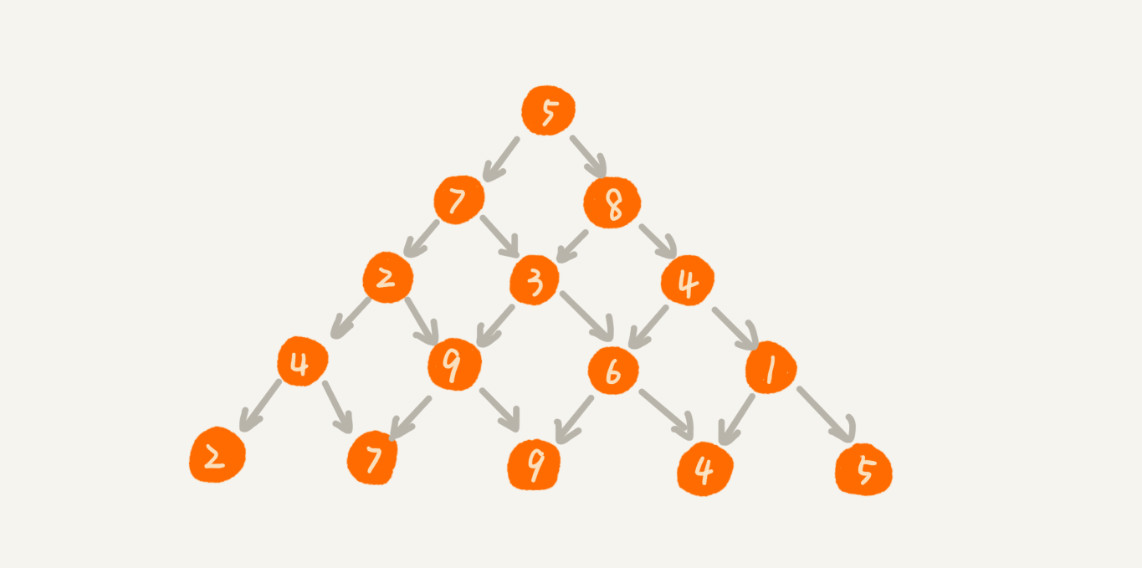40|初识动态规划：如何巧妙解决“双十一”购物时的凑单问题？ - 图4

贪心：一条路走到黑，就一次机会，只能哪边看着顺眼走哪边
回溯：一条路走到黑，无数次重来的机会，还怕我走不出来 (Snapshot View)
动态规划：拥有上帝视角，手握无数平行宇宙的历史存档， 同时发展出无数个未来 (Versioned Archive View)。
杨辉三角的动态规划转移方程是：S[i][j] = min(S[i-1][j],S[i-1][j-1]) + a[i][j]。
其中a表示到这个点的value值，S表示到a[i][j]这个点的最短路径值。
这里没有做边界条件限制，只是列出一个方程通式。边界条件需要在代码里具体处理。个人感觉动态规划的思想关键在于如何列出动态规划方程，有了方程，代码基本就是水到渠成了。
**