题目

中文

https://leetcode-cn.com/problems/climbing-stairs/
image.png

英文

https://leetcode.com/problems/climbing-stairs/
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?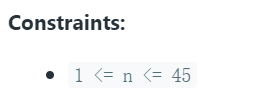
image.png

题解

第一遍

找最近重复子问题。

思路

第n阶f(n)的走法是由前面的走法加1步/2步推导来的。
1步的话则对应之前的f(n-1)
2步则对应之前的f(n-2)
以此递归。

n对应的是斐波那契数列的通项。
楼梯数 1 2 3 4
对应通项 1 1 2 3

所以如何解决斐波那契数列
1 递归绝对没问题
2 查斐波那契通项公式强行算。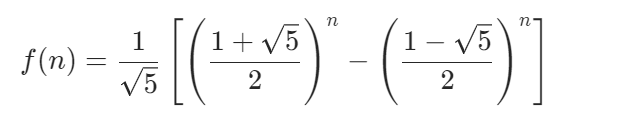
image.png

  1. int climbStairs(int n)
  2. {
  3.     if (n == 0)
  4.         return 0;
  5.     if (n == 1)
  6.         return 1;
  7.     else if (n == 2)
  8.         return 2;
  9.     else
  10.         return climbStairs(n - 1) + climbStairs(n - 2);
  11. }

O（2^n）
失败 超时了
所以简单点通项公式来一个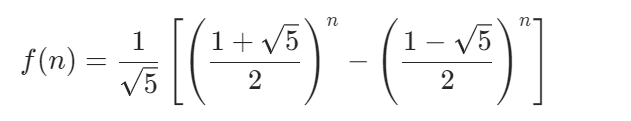
image.png
查他人题解发现这是动态规划 典型题。

本问题其实常规解法可以分成多个子问题，爬第n阶楼梯的方法数量，等于 2 部分之和

  • 爬上 n-1阶楼梯的方法数量。因为再爬1阶就能到第n阶
  • 爬上 n-2 阶楼梯的方法数量，因为再爬2阶就能到第n阶

所以我们得到公式 dp[n] = dp[n-1] + dp[n-2]
同时需要初始化 dp[0]=1 和 dp[1]=1
时间复杂度：O(n)O

  1. class Solution {
  2.     public int climbStairs(int n) {
  3.         int[] dp = new int[n + 1];
  4.         dp[0] = 1;
  5.         dp[1] = 1;
  6.         for(int i = 2; i <= n; i++) {
  7.             dp[i] = dp[i - 1] + dp[i - 2];
  8.         }
  9.         return dp[n];
  10.     }
  11. }

Java代码如图 还不熟练 所以码住留之后看。

解法1 循环递推 非递归 保留之前值

  1. int climbStairs(int n)
  2. {
  3.     if (n == 1)
  4.         return 1;
  5.     int n1 = 1;
  6.     int n2 = 2;
  7.     int temp;
  8.     for (int i = 3; i <= n; i++)
  9.     {
  10.         temp = n2;
  11.         n2 = n1 + n2;
  12.         n1=temp;
  13.     }
  14.     return n2;
  15. }

O(n)
n2=n1+n2;
所以要用一个数记住之前的n2; 即上一次的n2 这一次的n1.

一个更好理解的版本

  1. public int climbStairs(int n) {
  2.     // base cases
  3.     if(n <= 0) return 0;
  4.     if(n == 1) return 1;
  5.     if(n == 2) return 2;
  7.     int one_step_before = 2;
  8.     int two_steps_before = 1;
  9.     int all_ways = 0;
  11.     for(int i=2; i<n; i++){
  12.         all_ways = one_step_before + two_steps_before;
  13.         two_steps_before = one_step_before;
  14.         one_step_before = all_ways;
  15.     }
  16.     return all_ways;
  17. }