双指针

对撞指针

常用于元素反转

题目: 两数之和 II - 输入有序数组

解题思路:

• 数组从小到大排列, 双指针分别指向首部和尾部;

1. 首部尾部相加等于目标值，返回结果集
2. 首部尾部相加小于目标值，首部后移变大
3. 首部尾部相加大于目标值，尾部前移变小

实现:

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        vector<int> res;
        int l = 0, r = numbers.size() - 1;
        while(l <= r)
        {
            int sum = numbers[l] + numbers[r];
            if (sum == target)
            {
                res.push_back(l + 1);
                res.push_back(r + 1);
                break;
            }
            else if (sum < target) l++;
            else r--;
        }
        return res;
    }
};

快慢指针

对于每个同向双指针的题目需要考虑这么几个点:

1. 快指针什么时候移动？
2. 慢指针什么时候移动？
3. 快慢指针移动步数时候有联系？

题目: 移除元素

解题思路:

1. 快指针什么时候移动？目标值等于快指针对应下标的值时移动
2. 慢指针什么时候移动？目标值不等于快指针对应下标的值时, 将快指针对应下标的值赋给慢指针对应下标处的值
3. 快慢指针移动步数时候有联系？快指针指向的值不等于目标值时, 慢指针才移动

实现:

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slow = 0, fast = 0;
        while (fast < nums.size())
        {
            if (nums[fast] != val) nums[slow++] = nums[fast];
            fast++;
        }
        return slow;
    }
};

题目: 最大连续1的个数

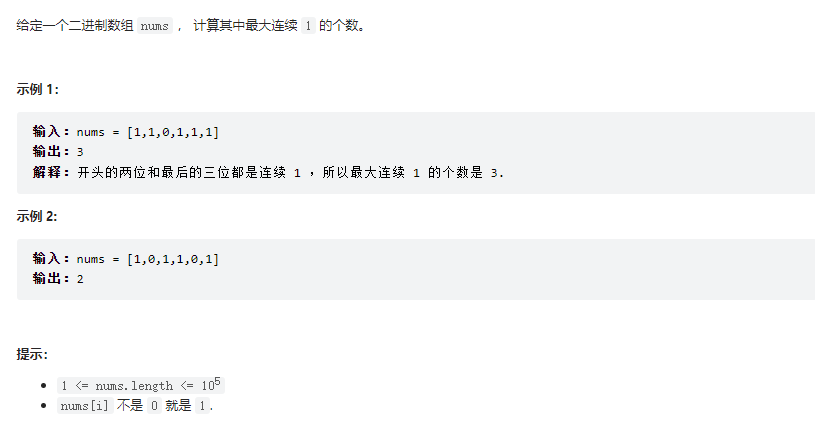
解题思路:

1. 快指针对应的值等于1时, 向前移动
2. 慢指针在快指针对应的值不等于1时, 根据快指针位置移动
3. 慢指针在判断完当前最大滑动窗口后, 指向快指针下一位

实现:

class Solution {
public:
    int findMaxConsecutiveOnes(vector<int>& nums) {
        int res = 0, l = 0, r = 0;
        while (r < nums.size())
        {
            if (nums[r] == 1) r++;
            else
            {
                res = max(r - l, res);
                l = ++r;
            }
        }
        res = max(r - l, res);
        return res;
    }
};

题目: 长度最小的子数组

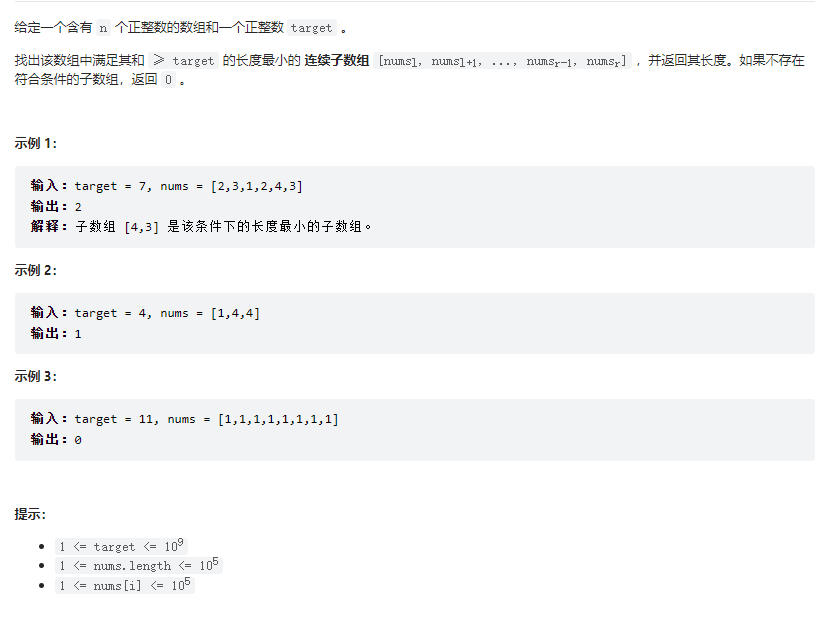
解题思路:

1. 快指针在局部之和小于target时, 向前移动
2. 局部之和大于等于target时, 向前移动
3. 快慢指针之间的长度再加1, 就是满足条件子数组的长度

实现:

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int len = nums.size();
        if (len == 0) return 0;
        int l = 0, r = 0, sum = 0, res = INT_MAX;
        while (r < len)
        {
            sum += nums[r];
            while (sum >= target)
            {
                res = min(res, r - l + 1);
                sum -= nums[l];
                l++;
            }
            r++;
        }
        return res == INT_MAX ? 0 : res;
    }
};

题目：环形链表

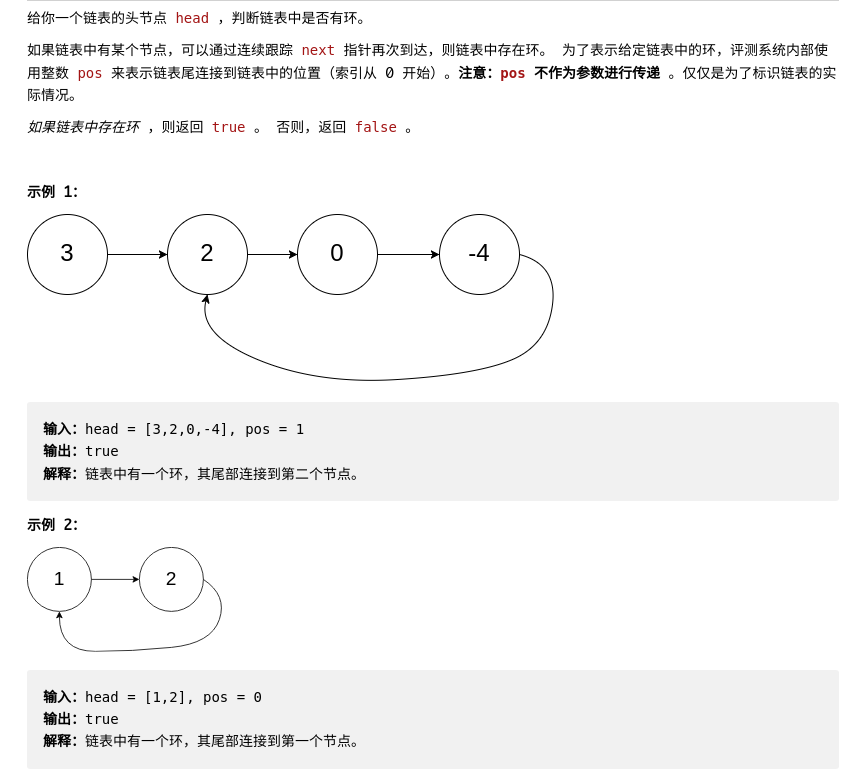
解题思路：
双指针
实现：

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while (fast != nullptr && fast->next != nullptr)
        {
            slow = slow->next;
            fast = fast->next->next;
            // if meet, the loop exist
            if (fast == slow) return true;
        }

        return false;
    }
};

题目：环形链表II

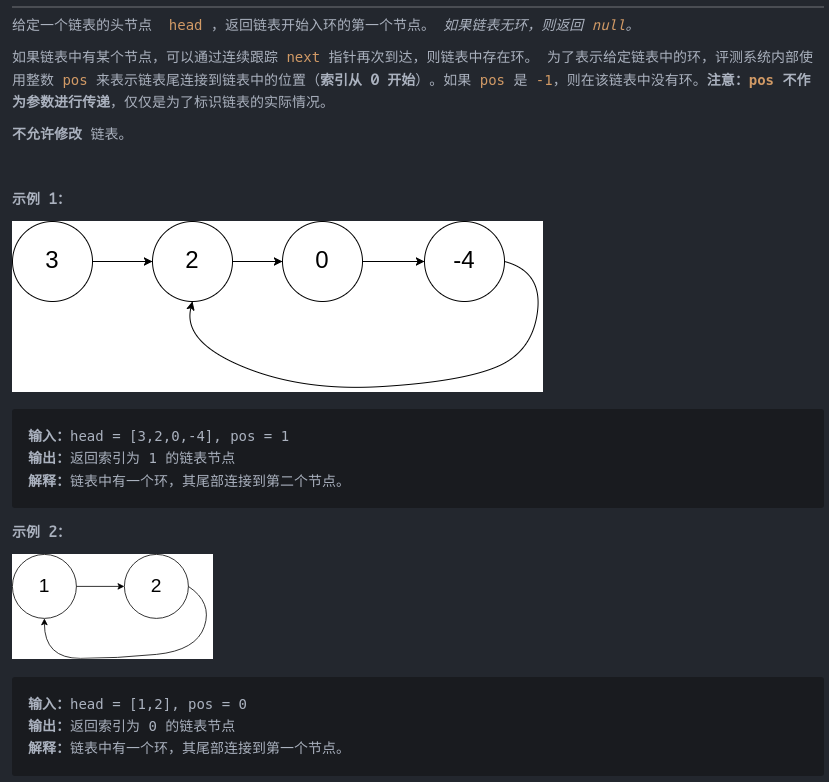
解题思路：
相遇时，fast一定比slow多走了
步， 假设相遇点距环的起点的距离为 m，那么结合上图的 slow 指针，环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后一定会相遇，相遇之处就是环的起点了。
实现：

/*
 * @lc app=leetcode.cn id=142 lang=cpp
 *
 * [142] 环形链表 II
 */

// @lc code=start
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *fast = head, *slow = head;
        while (fast != nullptr && fast->next != nullptr)
        {
            slow = slow->next;
            fast = fast->next->next;
            if (fast == slow) break;  // met
        }

        if (fast == nullptr || fast->next == nullptr) return nullptr;
        slow = head;
        while (slow != fast)
        {
            slow = slow->next;
            fast = fast->next;
        }

        return slow;
    }
};