复杂度分析（上） - 《数据结构与算法》

前言

复杂度分析包括：时间复杂度，空间复杂度。

数据结构与算法主要解决的问题：快（时间），省（空间）

复杂度分析为什么是必要的，可能有些人觉得实际运行查看结果就可以了，但这样是不准确的。因为这样得到的结果除了和代码执行效率有关，还和以下因素有关。

因此，我们需要一个不需要具体数据，只通过分析代码得到算法的执行效率。

把代码执行的单位时间称为单位时间，unit_time,T(n)称为总时间。其中n为执行次数。下面这段需要的总时间为(2n+2)*unit_time，与循环的次数成正比关系。

int cal(int n) {
  int sum = 0;
  int i = 1;
  for (; i <= n; ++i) {
    sum = sum + i;
  }
  return sum;
}

当是两个嵌套循环的时候，比如下面的代码：整段代码总的执行时间 T(n) = (2n2+2n+3)*unit_time.

int cal(int n) {
  int sum = 0;
  int i = 1;
  for (; i <= n; ++i) {
    sum = sum + i;
  }
  return sum;
}

上面的两个案例就可以表示为T(n) =O(fn), 在时间复杂度的时候，我们只保留最大量级，而忽略掉其他的低阶、常量、系数，因为这些不能左右时间的变化趋势，所以就写成T(n)=O(n),T(n)=O(n^2）

关注循环执行次数最多的一段代码，因为它的复杂度就是整段代码的复杂度。而这里的执行次数是指代码嵌套执行的次数。比如上面的例子中，分别是一层嵌套，两层嵌套，所以分别是复杂度为n，以及n^2的，明显的后面的复杂度要比前面的高。

当整段代码是两段代码的结合结果时，我们需要分析的是最大数量级的复杂度，它的复杂度就是多段代码的时间复杂度。也就是：总的时间复杂度就等于量级最大的那段代码的时间复杂度。

当两段代码互相嵌套时，其复杂度是两段代码的复杂度相乘。

提示：以上三种分析方法不用特别记忆，只要去分析代码，多看多分析就能的出代码的时间复杂度。

对于刚罗列的复杂度量级，我们可以粗略地分为两类，多项式量级和非多项式量级。其中非多项式量级只有O(2^n)以及O(n!).

当数据规模变得很大的时候，非多项式的效率会非常低，所以不推荐使用。这里暂时只介绍多项式时间复杂度的典型代码。

O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行1行，而是指执行固定次数。所以即使代码是执行3，5次，复杂度也是O(1).

 int i = 8;
 int j = 6;
 int sum = i + j;

小结：一般情况下，代码中不存在循环或者递归语句，我们都认为代码的复杂度是O(1).

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

可以看到其与普通循环的差别便是每次递增的幅度不是1，而是一个对数阶，所以其复杂度大大的降低。上面这段代码的复杂度便是O(log2n).而对数阶是可以互相转换的，所以可认为不同的对数阶复杂度也是一样的。

而如果在对数阶外层再有n层循环，复杂度便是O(nlogn),归并排序和快速排序的时间复杂度都是O(nlogn)。

加法的取决于m和n两个的数据规模谁大；

乘法的和乘法法则的一样，时间复杂度为相乘的关系。

其基本常识与时间复杂度一样，是指随着数据规模的变大，所占用的存储空间大小与n的关系。

空间复杂度与时间复杂度相比要简单很多，而且常见的空间复杂度只有O(1)、O(n)、O(n2 )，其他的很少见。

几乎所有的数据结构和算法都可以用这些来表示，我们用图解记录下其复杂度的大小关系。

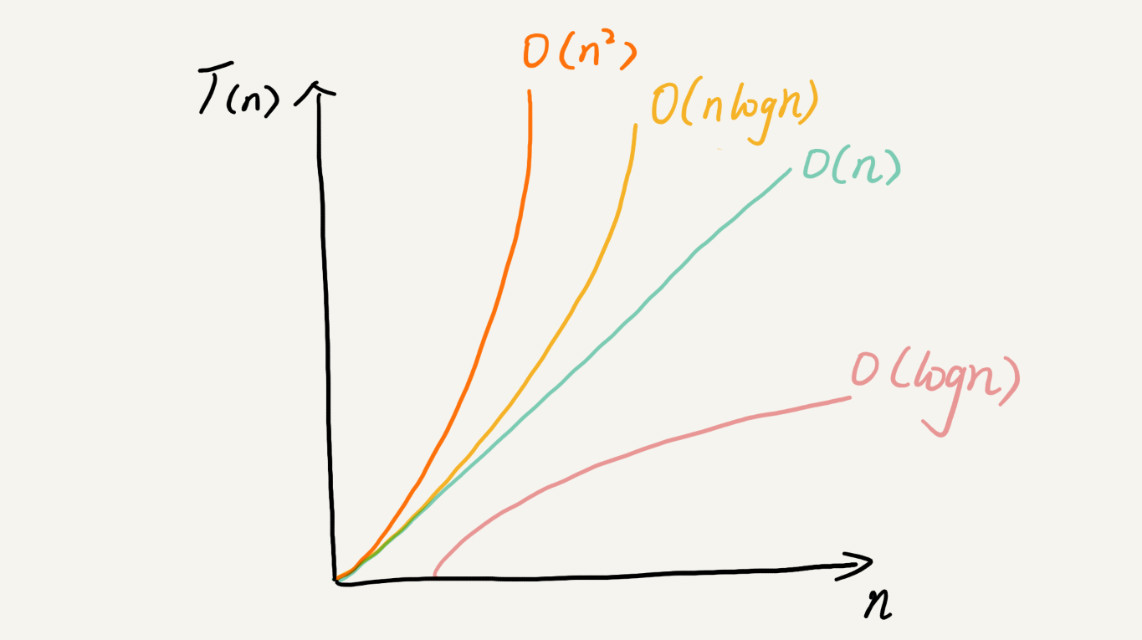
在之后的学习中，要多学多练便可以快速的掌握分析复杂度的窍门。