189. 轮转数组 - 翻转数组

题目链接

轮转数组

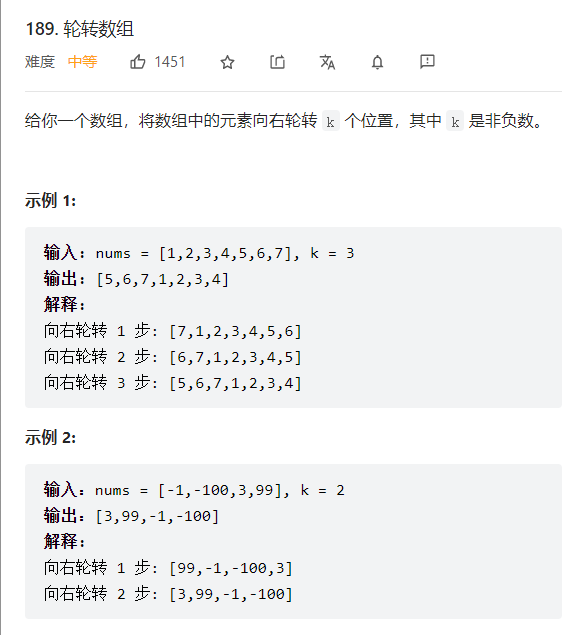
题目描述

解题思路

方法一：辅助数组

思路简单，直接上实现代码：

class Solution {
    public void rotate(int[] nums, int k) {
        int len = nums.length;
        int[] arr = new int[len];
        for(int i=0; i<len; i++) {
            arr[i] = nums[i];
        }
        // 找到1的位置
        int oneIndex = k % len;
        int arrIndex = 0;
        for(int i=oneIndex; i<len; i++) {
            nums[i] = arr[arrIndex++];
        }
        for(int i=0; i<oneIndex; i++) {
            nums[i] = arr[arrIndex++];
        }
    }
}

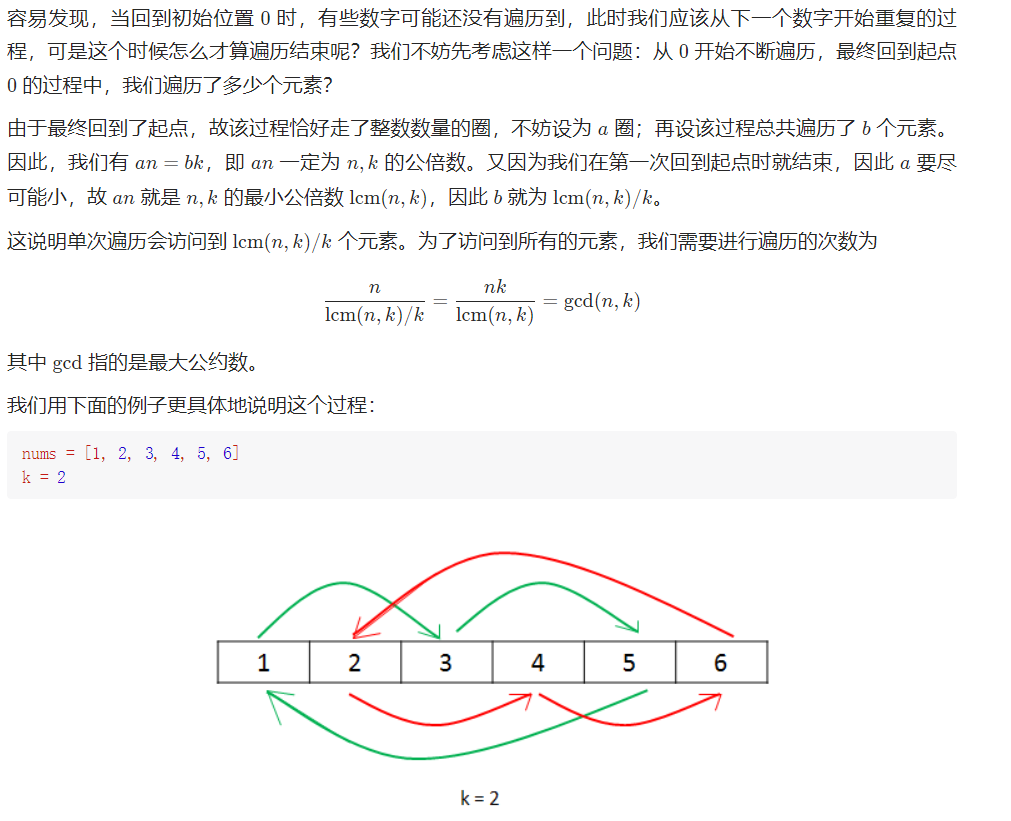
方法二：环形替换

假设替换i位置的元素，替换后的位置应该为：（i+ k）% len；这里不借用辅助数组开辟新的空间，每次替换保存替换位置的元素，然后进行下一轮元素查找替换；直到替换的位置回到原点，则继续往后进行替换，直到替换了n次；

实现代码：

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k = k % n;
        int count = gcd(k, n);
        for (int start = 0; start < count; ++start) {
            int current = start;
            int prev = nums[start];
            do {
                int next = (current + k) % n;
                int temp = nums[next];
                nums[next] = prev;
                prev = temp;
                current = next;
            } while (start != current);
        }
    }
    public int gcd(int x, int y) {
        return y > 0 ? gcd(y, x % y) : x;
    }
}

方法三：翻转数组

该方法基于如下的事实：当我们将数组的元素向右移动 k 次后，尾部 kmodn 个元素会移动至数组头部，其余元素向后移动 kmodn 个位置。

该方法为数组的翻转：我们可以先将所有元素翻转，这样尾部的 kmodn 个元素就被移至数组头部，然后我们再翻转 [0,kmodn−1] 区间的元素和[kmodn,n−1] 区间的元素即能得到最后的答案。

我们以 n=7，k=3 为例进行如下展示：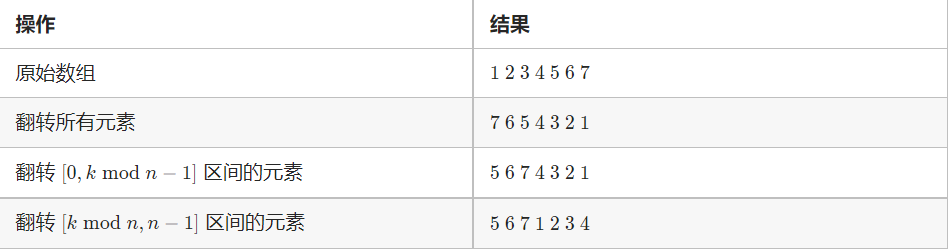

class Solution {
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start += 1;
            end -= 1;
        }
    }
}