函数式编程 2

命令式：一步一步地

def invertTree(root): 
    if root is None: 
        return None
    root.left, root.right = invertTree(root.right), invertTree(root.left) 
    return root

函数式：描述一下，声明式的

def invert(node): 
    if node is None: 
        return None 
    else 
        return Tree( node.value, invert(node.right), invert(node.left) )

好文章：
https://www.zhihu.com/question/28292740?sort=created
https://blog.csdn.net/weixin_34311757/article/details/88425474

数据的处理方式：

转换 - transform/map 数据由一种形式到另一种形式，R.compose/R.pipe 管道
聚合 - converge 多个数据求结果 R.converge
解析 - parse 一个数据分解出多个结果

通过纯函数，对各种类型的数据的各种处理。

函数式编程是一种编程的模式，在这种编程模式中最常用的函数和表达式。
它强调在编程的时候用函数的方式思考问题，函数也与其他数据类型一样，处于平等地位。
可以将函数作为参数传入另一个函数，也可以作为别的函数的返回值。
函数式编程倾向于用一系列嵌套的函数来描述运算过程。

Pointfree 的本质就是使用一些通用的函数，组合出各种复杂运算。上层运算不要直接操作数据，而是通过底层函数去处理。
这句话，很有道理！

Pointfree 就是运算过程抽象化，处理一个值，但是不提到这个值。这样做有很多好处，它能够让代码更清晰和简练，更符合语义，更容易复用，测试也变得轻而易举

跟shell管道思想有点像, 一个命令/方法只负责一件简单的事情, 最终组合在一起完成复杂的事情, 易维护, 易排错, 易开发.

Functional programming languages are a class of languages designed to reflect the way people think mathematically(以数学的方式思考), rather than reflecting the underlying machine. Functional languages are based on the lambda calculus ( https://en.wikipedia.org/wiki/Lambda_calculus ), a simple model of computation, and have a solid theoretical foundation that allows one to reason formally about the programs written in them.

The most commonly used functional languages are Standard ML, Haskell, and “pure” Scheme (a dialect of LISP), which, although they differ in many ways, share most of the properties described here. For a complete description of these languages and of functional programming in general, see Bird and Wadler [1988], Paulson[1991], Sussman and Abelson [1985], Hudak et al. [1992], Milner et al. [1990], Artificial Intelligence Laboratory[1992], and Hudak [1989].

In contrast to the usual imperative languages(命令式语言) (e.g., C, Fortran, and Ada), in which variables represent cells in memory that can be modified using the assignment operator (or :), functional languages view the use of the operator as an expression of an equation. For example, if a functional program contains the declaration

let x = f(y)

then this would introduce the name x and assert that the equation x = f(y) is true. There is no notion of a memory cell, and certainly no notion that somehow later in the program x might change (so that the equation would become false).

If one were to write

let x = x + 1

in a functional program, this would represent an equation with no finite solution (and would either be rejected by acompiler or result in a nonterminating computation), whereas in C this would increment the contents of the memory cell denoted by x.

Function names are introduced in a similar way. The declaration

let f(x, y) = x + y

introduces the function f and states that f(x, y) and x + y are equal, for any x and y. The expression on the right-hand side, the body of f, cannot be a sequence of statements modifying the values of x and y (and perhaps other variables). As in mathematics, a function is a single-valued relation such that, given the same argument(s), it will return the same result(对外界无副作用). This is certainly not the case in the imperative programs.

Because variables in a functional program cannot be modified, repetition must be expressed in a functional program via recursion rather than through the use of loops. Consider the factorial function, defined formally as: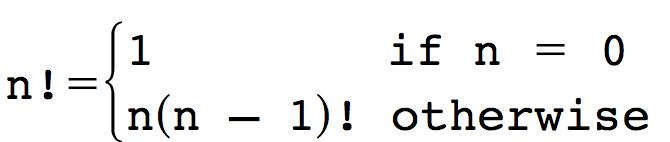

In a functional language the executable definition of factorial is generally written as

and follows directly from the formal definition (where == is the equality comparison operator).

This is in contrast to the C version

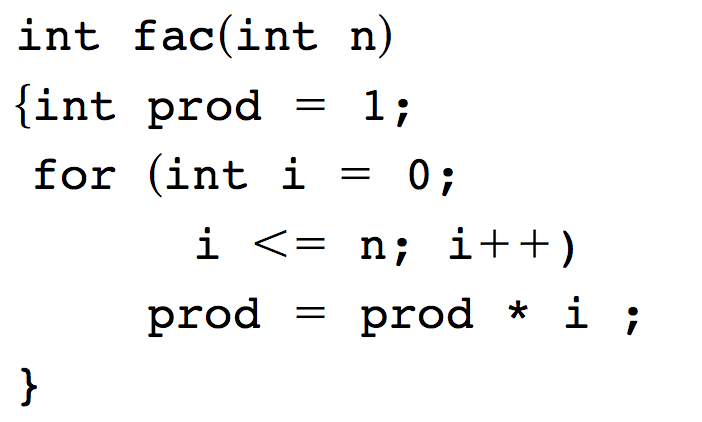
which can be understood only by tracing the sequence of modifications to the variables prod and i during the iteration.

Functional languages exhibit a property called referential transparency, which essentially means that “like can be replaced by like.” For example, the expression

f(y) + f(y)

is equivalent to

let x = f(y)
in x + x

in which the two original occurrences of f(y) are replaced by x. This follows directly from the fact that the declaration x = f(y) denotes an equation in a functional language, but certainly would not be the case in an imperative language. In an imperative language, the first call to f might change the value of a variable used in the second call to f. This kind of behavior, known as a side-effect, cannot occur in a functional language.

HIGHER-ORDER FUNCTIONS

Most functional languages support functions that operate over functions—that is, functions that take other functions as parameters and/or return functions as values. A simple example is the compose function, defined as

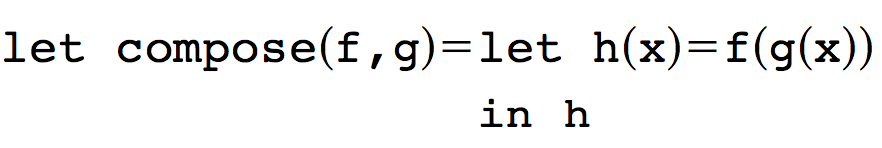
In this case, the parameters to compose, f, and g, must both be functions. In addition, the value returned by compose, namely h, is also a function, defined by the equation h(x) = f(g(x)).

As another example of the use of higher-order functions, consider again the factorial function. It might be argued that the formal definition of factorial given above was tailored to suit the recursive nature of the definition of factorial in the functional language, and that a more reasonable and common definition of factorial is

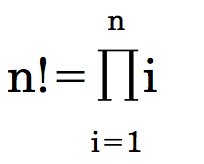
The product operator, , is a very useful operator that has the general form:

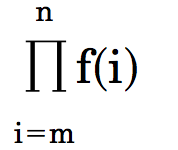
for some initial value m, some final value n, and some function f. In a functional language, 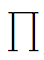can easily be written as a higher-order function of three parameters, m, n, and f, defined by

where == is the equality comparison operator. Thus, factorial can be defined as:

and the power function, computing 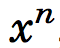,can be defined as

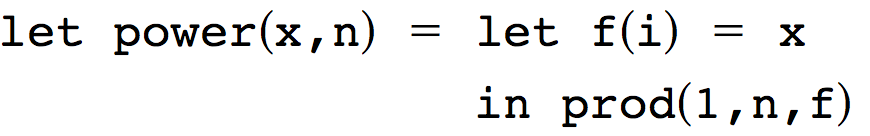
NON-STRICT FUNCTIONAL LANGUAGES

In most programming languages, a function call of the form

causes the argument expressions , to be evaluated before the body of the function f is executed. This is also the case in ML and Scheme. However, in a class of functional languages called non-strict functional languages, of which Haskell is the most popular, no function evaluates its arguments unless they are needed(按需求值). For example, the function f defined by

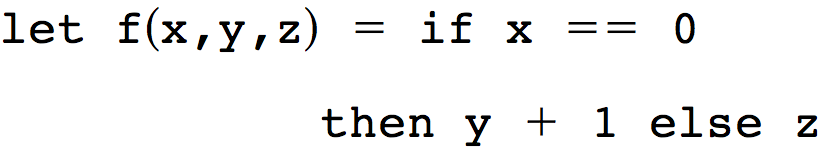
always evaluates its first, parameter, x, but only one of y or z will be evaluated. Thus, in the call

f(4, g(3), h(2))

the expression g(3) will not be evalu-ated.

Non-strictness is attractive for two reasons. First, it frees the programmer from worrying about various issues of control, such as choosing the correct order of evaluation among various expressions. In a non-strict language, an expression program won’t be evaluated unless it is needed. For example, in a producer-consumer problem, the producer is guaranteed to produce only what the consumer needs.

Another feature of non-strictness is that it allows the construction of infinite data structures. To see this, consider the recursive definition

let ones = 1 :: ones

where the :: operator constructs a list whose first element is the left operand, in this case 1, and whose subsequent elements come from the right operand, in this ones. That is, ones is a list that isrecursively defined to be 1 followed by allthe element of ones. Clearly, the only solution to this equation is if ones is the infinite list of 1’s. In a strict language, where :: requires the value of its arguments, the evaluation of the right-handside of the equation would never terminate. However, in a non-strict language, the :: does not evaluate its operands untilthey are actually needed. Ultimately, onlythose elements of ones that are required by other parts of the programs will becomputed. The rest of ones (which is infinite) would be left uncomputed.

RESEARCH ISSUES IN FUNCTIONALLANGUAGES

The functional language research community is very active in a number of areas. Of particular, interest is improving the speed of functional language implementations. There are two primary approaches: through compiler-based program analysis and optimization techniques, and through the execution of functional programs onparallel computers. Another area of research attempts to increase the expressiveness of functional languages for applications in which the notion of state and the change of state (through assignment) is seen as necessary in conventional programs. New constructs have been proposed that, although they appear to be side-effect operators such as array updates, actually preserve the referential transparency property.

作者：

BENJAMIN GOLDBERG

New York University goldberg@cs.nyu.edu