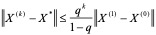第四章 解线性方程组的迭代法

第四章 解线性方程组的迭代法

对于阶数不高的方程组，直接法非常有效，对于阶数高，而系数矩阵稀疏的线性方程组却存在着困难，在这类矩阵中，非零元素较少，若用直接法求解，就要存贮大量零元素。为减少运算量、节约内存，使用迭代法更有利。本章介绍迭代法的初步内容。

§1 雅克比法、赛得尔法、超松驰法

1．雅克比（Jacobi）迭代法
设有n阶方程组
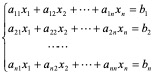（4.1）
若系数矩阵非奇异，且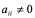 (i = 1, 2,…, n)，将方程组（4.1）改写成

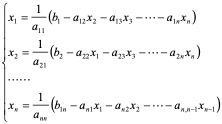
然后写成迭代格式
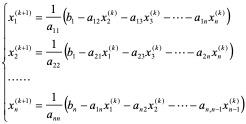（4.2）
（4.2）式也可以简单地写为
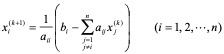（4.3）
对（4.2）或（4.3）给定一组初值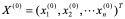后，经反复迭代可得到一向量序列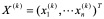，如果X__k收敛于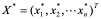，则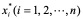就是方程组（4.1）的解。这一方法称为雅克比（Jacobi）迭代法或简单迭代法，（4.2）或（4.3）称为Jacobi迭代格式。
下面介绍迭代格式的矩阵表示：
设D = diag (a, a, …, a)，将方程组AX = b中的系数矩阵表示成三个特殊矩阵的代数和矩阵：
A = D –L-U
其中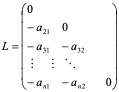
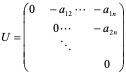
由于 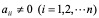，D为可逆对角阵，L、U分别为严格上、下三角阵，于是

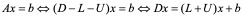
利用D可逆，得到等价方程组

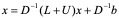
则迭代格式的向量表示为

，
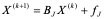
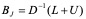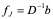
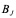称为雅克比迭代矩阵。
2．高斯――赛得尔（Gauss-Seidel）迭代法
显然，如果迭代收敛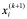，应该比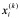更接近于原方程的解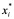（i = _1, 2,…, _n），因此在迭代过程中及时地以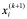代替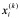（i = _1, 2,…, _n-1），可望收到更好的效果。这样（4.2）式可写成：
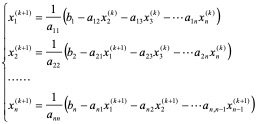（4.5）
（4.5）式可简写成
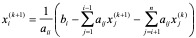（i = _1, 2,…, _n）
此为G－S迭代格式。
G－S迭代格式的矩阵表示：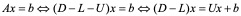


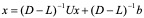
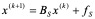（4.6）
，
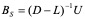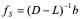
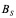称为高斯-赛德尔迭代矩阵。
关于上述迭代法的误差控制，可按类似于第二章非线性方程求根的迭代法处理，设e为允许的绝对误差限，可以检验

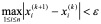
是否成立，以决定计算是否终止，进一步的讨论稍后进行。
实际计算时，如果线性方程组的阶数不高，建立迭代格式也可以不从矩阵形式出发，以避免求逆矩阵的计算。
3．超松驰法
使用迭代法的困难是计算量难以估计，有些方程组的迭代格式虽然收敛，但收敛速度慢而使计算量变得很大。
松驰法是一种线性加速方法。这种方法将前一步的结果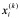与高斯――赛得尔方法的迭代值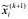适当进行线性组合，以构成一个收敛速度较快的近似解序列。改进后的迭代方案是：
迭代

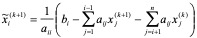
加速

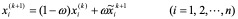
所以
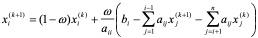（4.7）
这种加速法就是松驰法。其中系数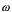称松驰因子。可以证明，要保证迭代格式（4.7）收敛必须要求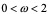
当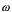 = 1时，即为高斯――赛得尔迭代法，为使收敛速度加快，通常取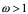，即为超松驰法。
松驰因子的选取对迭代格式（4.7）的收敛速度影响极大。实际计算时，可以根据系数矩阵的性质，结合经验通过反复计算来确定松驰因子。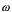
§2 迭代法的收敛条件

由§1中迭代格式的矩阵形式知，方程组AX = b的雅克比迭代法、高斯――赛得尔迭代法和松驰法的矩阵形式都可以写成下式：
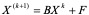（4.8）
当然，不同的迭代法其迭代矩阵B和F的元素是不同的。所以我们讨论迭代格式（4.8）的收敛性，就具有普遍意义。
下面，我们不加证明地给出迭代格式（4.8）收敛的充分必要条件。
定理1：对任意初始向量X及常向量F，迭代格式（4.8）收敛的充分必要条件是迭代矩阵B的谱半径r(B) < 1。
这一结论在理论上是颇为重要的，但实际用起来不甚方便，为此我们着重研究更为实用的判别迭代格式收敛的充分条件。
考虑迭代向量序列{Xk)}的收敛问题：
若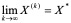

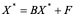
于是

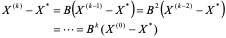
收敛的意思是：

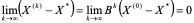
依范数收敛是
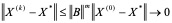当k®¥，从而得以下定理：
定理2：若迭代矩阵Ｂ的某种范数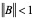则（4.8）确定的迭代法对任意初值X均收敛于方程组X = BX + F的唯一解x。
下面给出直接计算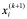时的收敛性定理。为给出这个定理，先介绍对角占优的概念。
定义1：如果矩阵的每一行中，不在主对角线上的所有元素绝对值之和小于主对角线上元素的绝对值，即

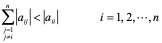
则称矩阵A按行严格对角占优，类似地，也有按列严格对角占优。
*定理3：若线性方程组AX = b的系数矩阵A按行严格对角占优，则雅克比迭代法和高斯――赛得尔迭代法对任意给定初值均收敛。
证明：记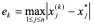
为第k次近似值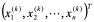的误差，
（1）由雅克比迭代法

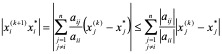
记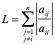
则有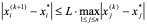
上式对 i = _1, 2,…, _n成立，故有

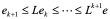
因为A严格对角占优，故L < 1，从而有

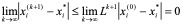
即雅克比方法收敛。
（2）高斯――赛得尔迭代法
考虑高斯――赛得尔方法的误差

记
则

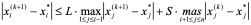
从而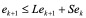

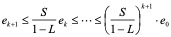
而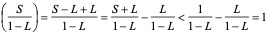
所以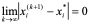
即：高斯――赛得尔迭代法收敛。 证完
例：用雅克比迭代法和高斯――赛得尔迭代法解线性方程组

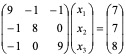
解：所给线性方程组的系数矩阵按行严格对角占优，故雅克比迭代法和高斯――赛得尔迭代法都收敛。
D = _diag (9, 8, 9) _D-1 = diag (1/9, 1/8, 1/9)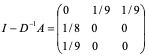

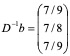
雅克比迭代法的迭代公式为：

取X = (0, 0, 0)T，由上述公式得逐次近似值如下：

k	0	1	2	3	4
X (i)

高斯――赛得尔迭代法：

迭代结果为：

k	0	1	2	3	4
x(i)

如果矩阵A严格对角占优，那么高斯――赛得尔迭代法的收敛速度快于雅克比迭代法的收敛速度。
以上定理2、3只是雅克比迭代法和高斯――赛得尔迭代法收敛的充分条件，对于一个给定的系数矩阵A，两种方法可能都收敛，也可能都不收敛；还可能是雅克比方法收敛而高斯――赛得尔方法不收敛；亦或相反。在计算机上，高斯――赛得尔方法只需要一套存放迭代向量的单元，而雅克比方法都需两套。
§3 迭代法的误差估计
在§1中曾以检验

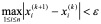
是否成立的办法来估计误差并确定迭代是否终止。它的理论依据是：
定理4：设X是方程组AX = b的同解方程X = BX + F的准确解，若迭代公式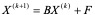中迭代矩阵B的某种范数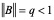，则有
1）
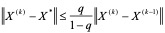
2）
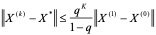
证明：先证1）因为
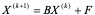（4.9）
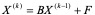（4.10）
由（4.9）、（4.10）相减得
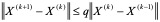（4.11）
因为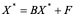，故

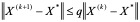
另一方面，

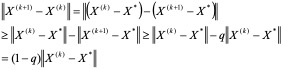
再由（4.11）便得:
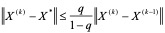（4.12）
反复运用（4.11）可得
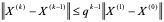（4.13）
将（4.13）代入（4.12）即有