Given an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Q：给定一个字符表，判断某单词是否在表格中出现。表格中的每个字符最多使用一次，下一个字符必须是上一个字符的相邻字符。

Constraints:

  • m == board.length
  • n = board[i].length
  • 1 <= m, n <= 6
  • 1 <= word.length <= 15
  • board and word consists of only lowercase and uppercase English letters.

Example 1: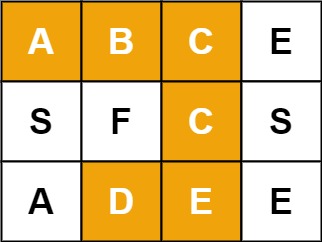
image.png
**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
**Output:** true
Example 2: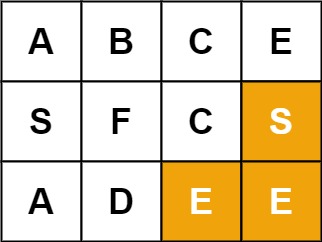
image.png
**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
**Output:** true
Example 3:
image.png
**Input:** board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
**Output:** false

方法：深度优先搜索

  1. class Solution {
  2. public:
  4.     class Point{
  5.     public:
  6.         int x;           // 行索引
  7.         int y;           // 列索引
  8.         int d;           // 方向索引
  10.         Point():x(0), y(0), d(0){}
  11.         Point(int _x, int _y):x(_x), y(_y), d(0){}
  12.     };
  14.     bool exist(vector<vector<char>>& board, string word) {
  15.         if(word.length() <= 0){
  16.             return true;
  17.         }
  18.         int n = board.size(), m = board[0].size();
  19.         stack<Point> path;
  21.         for(int i=0; i<n; i++){
  22.             for(int j=0; j<m; j++){
  23.                 if(board[i][j] == word[0] && dfs(board, word, i, j)){
  24.                     return true;
  25.                 }
  26.             }
  27.         }
  28.         return false;
  29.     }
  31.     bool dfs(vector<vector<char>>& board, string& word, int i, int j){
  32.         // 在索引i、j处深度优先搜索，查找word
  33.         // 已知 board[i][j] == word[0]
  34.         int n = board.size(), m = board[0].size();
  35.         int offset[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
  37.         stack<Point> path;
  38.         vector<vector<bool>> visited(n, vector<bool>(m, false));
  40.         path.push(Point(i, j));
  41.         visited[i][j] = true;
  43.         while(path.size() < word.length()){
  44.             Point& cp = path.top();
  46.             if(cp.d >= 4){
  47.                 // cp的四个方向都访问过，都不行，需要退出当前节点，回到上一个节点
  48.                 visited[cp.x][cp.y] = false;
  49.                 path.pop();
  50.                 if(path.empty()){
  51.                     return false;
  52.                 }
  53.             }
  54.             else{
  55.                 Point np;
  56.                 np.x = cp.x + offset[cp.d][0];
  57.                 np.y = cp.y + offset[cp.d][1];
  58.                 cp.d += 1;                // 下次再访问该点时的下一个相邻方向
  60.                 if(isIn(np, n, m) && !visited[np.x][np.y] && board[np.x][np.y] == word[path.size()]){
  61.                     // 下一个位置在内部、未访问过、且是下一个要访问的字符
  62.                     path.push(np);
  63.                     visited[np.x][np.y] = true;
  64.                 }
  65.             }
  66.         }
  67.         return true;
  68.     }
  70.     bool isIn(Point p, int n, int m){
  71.         if(p.x >= 0 && p.x < n && p.y >= 0 && p.y < m){
  72.             return true;
  73.         }
  74.         return false;
  75.     }
  76. };

运行效率评价：

Success Details
Runtime: 752 ms, faster than 17.20% of C++ online submissions for Word Search.
Memory Usage: 7.8 MB, less than 5.08% of C++ online submissions for Word Search.