题目链接：

题目大意：

给定一棵树，有n个点，每个点（假设点为v）给定两个值分别是lv和rv，再给定n-1条边，对于每条边来说它的贡献值是|ai - aj|，i 和 j 是边的两个点，ai 是介于 li 和 ri 之间的任意一个值，aj 同理。 求这个树最大的贡献值是多少。

解题思路：

第一时间的想法就是每个点必须选取极端的值，因为对于任意边来说，两点差的绝对值最大肯定是极端值的情况。
以Test case 3的4，6讨论一下：

  1. 很明显4，6的最大贡献值要选取2和17
  2. 如果不这么选而选取中间值，那就只有一个理由：2和3的那条边影响到了4
  3. 但是下面那条边如果想要选取出最大贡献，也要取极端值
  4. 而如果6号点选取了中间值，那很明显对于4和6的贡献都不是最大的
  5. 什么，2和4也不选取极端值，那你可以选择暴力枚举出来，6、2、3他们的贡献值一定没刚才大

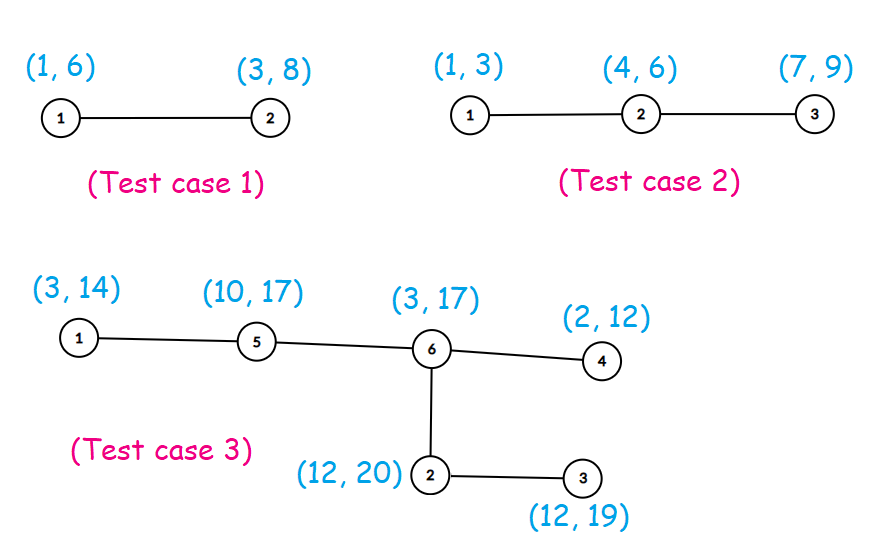
cf：Parsa's Humongous Tree - 图1

当然，上面只是为了说明选取极端值才是最好的，并不是最重要的东西。
只有选取极端值我们才可以用dp来做。（不然枚举的第二维太多了，1e9存都存不下）

还以Test case 3的6、4、2、3举例，他们的最大贡献无非就是左右枚举一遍，即(3，2，12，12）、（3，12，20，19）。。。。。
那么爆搜一遍答案其实就出来了，并且是正确的，如下：

TLE代码：

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. const int N = 1e5 + 50;
  4. typedef long long LL;
  6. int e[N], ne[N], h[N], idx;
  8. void add(int a, int b)
  9. {
  10.     e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
  11. }
  13. int l[N], r[N];
  15. int t, n;
  17. int f[N];
  19. int dfs(int u, int cs, int f) {
  20.     int dist = 0;
  21.     for (int i = h[u]; ~i; i = ne[i]) {
  22.         int j = e[i];
  23.         if (j == f) continue; // 防止死循环
  24.         // 就是这里，选取相邻结点的两个极端值即可
  25.         dist += max(dfs(j, l[j], u) + abs(cs - l[j]), dfs(j, r[j], u) + abs(cs - r[j]));
  26.     }
  27.     return dist;
  28. }
  30. int main()
  31. {
  32.     cin >> t;
  33.     while (t -- ) {
  34.         memset(h, -1, sizeof h);
  35.         scanf("%d", &n);
  36.         for (int i = 1; i <= n; i ++ ) scanf("%d%d", &l[i], &r[i]);
  37.         for (int i = 0; i < n - 1; i ++ ) {
  38.             int a, b;
  39.             scanf("%d%d", &a, &b);
  40.             if (a > b) swap(a, b);
  41.             add(a, b);
  42.             add(b, a);
  43.         }
  44.         printf("%d\n", max(dfs(1, l[1], -1), dfs(1, r[1], -1)));
  46.     }
  47.     return 0;
  48. }

但是很容易发现，这个复杂度是指数级别的，所以我很快啊，啪的一下就TLE了。。 仔细看其实这个代码是从上往下找的，即要往左找一遍，往右找一遍，这才导致复杂度高。 如果先处理出来子节点的左右max值，当前节点直接用，就变成了线性 可以这么做的原因是并不像传统的二叉树有两个儿子，这题只有一个儿子，但是有两个值而已

AC代码：

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. typedef long long LL;
  4. const int N = 1e6 + 20;
  5. int n;
  6. int e[N], ne[N], h[N], idx;
  7. LL l[N], r[N];
  9. void add(int a, int b) {
  10.     e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
  11. }
  13. int t;
  15. LL dp[N][2];
  17. void dfs(int u, int f) {
  18.     dp[u][0] = dp[u][1] = 0;
  19.     for (int i = h[u]; ~i ; i = ne[i]) {
  20.         int j = e[i];
  21.         if (j == f) continue;
  22.         // 这里让他先递归下去，记录下以j为根的最优解
  23.         dfs(j, u);
  24.         // 这里方程没变，直接用就可以了
  25.         // 此时递归两次变成了递归一次，但是一次就记录了最优解
  26.         dp[u][0] += max(dp[j][0] + abs(l[u] - l[j]), dp[j][1] + abs(l[u] - r[j]));
  27.         dp[u][1] += max(dp[j][0] + abs(r[u] - l[j]), dp[j][1] + abs(r[u] - r[j]));
  28.     }
  29. }
  31. int main()
  32. {
  33.     cin >> t;
  34.     while (t -- ) {
  35.         memset(h, -1, sizeof h);
  36.         scanf("%d", &n);
  38.         for (int i = 1; i <= n; i ++ ) scanf("%d%d", &l[i], &r[i]);
  39.         for (int i = 0; i < n - 1; i ++ ) {
  40.             int a, b;
  41.             scanf("%d%d", &a, &b);
  42.             add(a, b);
  43.             add(b, a);
  44.         }
  45.         dfs(1, -1);
  46.         printf("%lld\n", max(dp[1][0], dp[1][1]));
  47.     }
  49.     return 0;
  50. }