FFT前言

快速傅里叶变换 (fast Fourier transform),即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少，特别是被变换的抽样点数N越多，FFT算法计算量的节省就越显著。
FFT（Fast Fourier Transformation） 是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

FFT（Fast Fourier Transformation），中文名快速傅里叶变换，用来加速多项式乘法
朴素高精度乘法时间FFT快速傅里叶变换 - 图1，但FFT能FFT快速傅里叶变换 - 图2的时间解决。

多项式的系数表示法和点值表示法

  • FFT其实是一个用FFT快速傅里叶变换 - 图3的时间将一个用系数表示的多项式转换成它的点值表示的算法

  • 多项式的系数表示和点值表示可以互相转换

系数表示法

一个n-1次n项多项式FFT快速傅里叶变换 - 图4可以表示为 FFT快速傅里叶变换 - 图5
也可以用每一项的系数来表示FFT快速傅里叶变换 - 图6，即 FFT快速傅里叶变换 - 图7
这就是系数表示法.

点值表示法

  • 把多项式放到平面直角坐标系里面，看成一个函数
  • 把FFT快速傅里叶变换 - 图8个不同FFT快速傅里叶变换 - 图9的代入，会得出FFT快速傅里叶变换 - 图10个不同的FFT快速傅里叶变换 - 图11，在坐标系内就是FFT快速傅里叶变换 - 图12个不同的点
  • 那么这FFT快速傅里叶变换 - 图13个点唯一确定该多项式，也就是有且仅有一个多项式满足FFT快速傅里叶变换 - 图14
  • 理由很简单，把FFT快速傅里叶变换 - 图15条式子联立起来成为一个有FFT快速傅里叶变换 - 图16条方程的FFT快速傅里叶变换 - 图17元方程组，每一项的系数都可以解出来，那么FFT快速傅里叶变换 - 图18

这就是点值表示法。

高精度乘法下两种多项式表示法的区别

对于两个用系数表示的多项式，我们把它们相乘设两个多项式分别为FFT快速傅里叶变换 - 图19，我们要枚举A每一位的系数与B每一位的系数相乘，那么系数表示法做多项式乘法时间复杂度FFT快速傅里叶变换 - 图20。
但两个用点值表示的多项式相乘，只需要FFT快速傅里叶变换 - 图21的时间。

设两个点值多项式分别为
FFT快速傅里叶变换 - 图22
设它们的乘积是FFT快速傅里叶变换 - 图23，那么
FFT快速傅里叶变换 - 图24
所以这里的时间复杂度只有一个枚举的FFT快速傅里叶变换 - 图25

  • 朴素系数转点值的算法叫DFT（离散傅里叶变换），点值转系数叫IDFT（离散傅里叶逆变换）

DFT（离散傅里叶变换）

一定注意从这里开始所有的n都默认为2的整数次幂
对于任意系数多项式转点值，当然可以随便取任意n个x值代入计算
但是暴力计算FFT快速傅里叶变换 - 图26当然是FFT快速傅里叶变换 - 图27的时间
其实可以代入一组神奇的x，代入以后不用做那么多的次方运算
这些x当然不是乱取的，而且取这些x值应该就是傅里叶的主意了

考虑一下，如果我们代入一些x，使每个x的若干次方等于1，我们就不用做全部的次方运算了
± 1是可以的，考虑虚数的话± i也可以，但只有这四个数远远不够

傅里叶说：这个圆圈上面的点都可以做到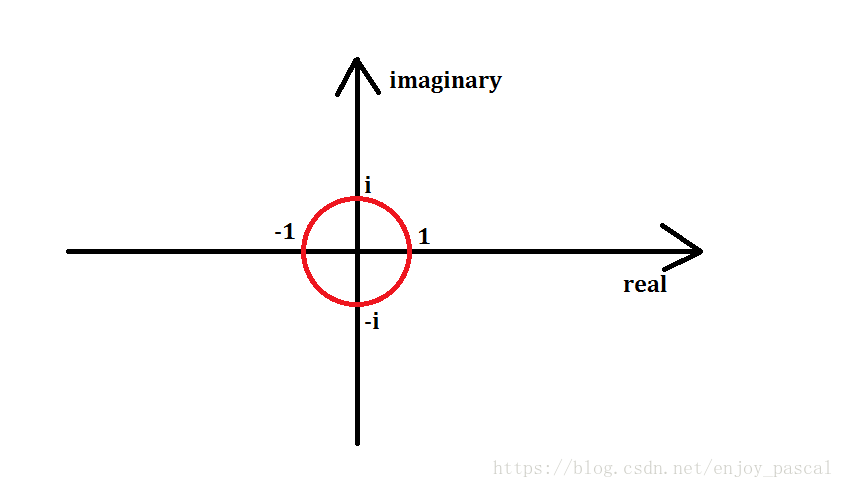
image.png
以原点为圆心，画一个半径为1的单位圆，那么单位圆上所有的点都可以经过若干次次方得到1，傅里叶说还要把它给n等分了，比如此时n = 8

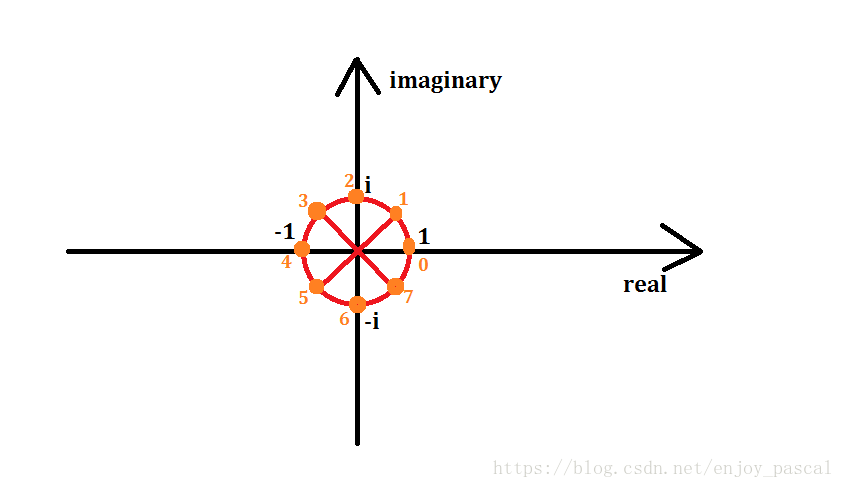
image.png
橙色点即为n = 8时要取的点，从( 1 , 0 ) 点开始，逆时针从0号开始标号，标到7号
记编号为k的点代表的复数值为FFT快速傅里叶变换 - 图30，那么由模长相乘，极角相加可知FFT快速傅里叶变换 - 图31
其中FFT快速傅里叶变换 - 图32称为n次单位根，而且每一个FFT快速傅里叶变换 - 图33都可以求出 。
FFT快速傅里叶变换 - 图34
那么 FFT快速傅里叶变换 - 图35 即为我们要代入的FFT快速傅里叶变换 - 图36

卷积

卷积与傅里叶变换有着密切的关系。利用一点性质，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，能使傅里叶分析中许多问题的处理得到简化。
FFT快速傅里叶变换 - 图37
其中F为傅里叶变换。

单位根的性质

  • FFT快速傅里叶变换 - 图38
  • FFT快速傅里叶变换 - 图39
  • FFT快速傅里叶变换 - 图40

FFT（快速傅里叶变换）

虽然DFT搞出来一堆很牛逼的FFT快速傅里叶变换 - 图41作为代入多项式的x值
但只是代入这类特殊x值法的变换叫做DFT而已，还是要代入单位根暴力计算

  • DFT还是暴力FFT快速傅里叶变换 - 图42…

但DFT可以分治来做，于是 FFT（快速傅里叶变换） 就出来了
首先设一个多项式FFT快速傅里叶变换 - 图43
按FFT快速傅里叶变换 - 图44下标的奇偶性把FFT快速傅里叶变换 - 图45分成两半，右边再提一个x
FFT快速傅里叶变换 - 图46
FFT快速傅里叶变换 - 图47
两边好像非常相似，于是再设两个多项式FFT快速傅里叶变换 - 图48，令
FFT快速傅里叶变换 - 图49
FFT快速傅里叶变换 - 图50
比较明显得出
FFT快速傅里叶变换 - 图51

再设FFT快速傅里叶变换 - 图52，把 FFT快速傅里叶变换 - 图53作为x代入FFT快速傅里叶变换 - 图54（接下来几步变换要多想想单位根的性质）

FFT快速傅里叶变换 - 图55
那么对于FFT快速傅里叶变换 - 图56的话，代入 FFT快速傅里叶变换 - 图57
FFT快速傅里叶变换 - 图58

如果已知FFT快速傅里叶变换 - 图59和FFT快速傅里叶变换 - 图60的值，我们就可以同时知道FFT快速傅里叶变换 - 图61和FFT快速傅里叶变换 - 图62的值
现在我们就可以递归分治来求FFT。
每一次回溯时只扫当前前面一半的序列，即可得出后面一半序列的答案n==1时只有一个常数项，直接return
时间复杂度FFT快速傅里叶变换 - 图63
image.png

IFFT（快速傅里叶逆变换）

想一下，我们不仅要会FFT，还要会IFFT（快速傅里叶逆变换）我们把两个多项式相乘 （也叫求卷积），做完两遍FFT也知道了积的多项式的点值表示
可我们平时用系数表示的多项式，点值表示没有意义

  • 怎么把点值表示的多项式快速转回系数表示法?
  • IDFT暴力FFT快速傅里叶变换 - 图65做？其实也可以用FFT用FFT快速傅里叶变换 - 图66的时间做
  • 一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以n即为原多项式的每一项系数

FFT模板

  1. #include <bits/stdc++.h>
  2. #define ll long long
  3. using namespace std;
  4. const int N = 1e6+10;
  5. const double PI = acos(-1.0);
  6. struct Complex
  7. {
  8.     double r,i;
  9.     Complex(double _r = 0,double _i = 0)
  10.     {
  11.         r = _r; i = _i;
  12.     }
  13.     Complex operator +(const Complex &b)
  14.     {
  15.         return Complex(r+b.r,i+b.i);
  16.     }
  17.     Complex operator -(const Complex &b)
  18.     {
  19.         return Complex(r-b.r,i-b.i);
  20.     }
  21.     Complex operator *(const Complex &b)
  22.     {
  23.         return Complex(r*b.r-i*b.i,r*b.i+i*b.r);
  24.     }
  25. };
  26. void change(Complex* y,int len)
  27. {
  28.     int i,j,k;
  29.     for(i = 1, j = len/2;i < len-1;i++)
  30.     {
  31.         if(i < j)swap(y[i],y[j]);
  32.         k = len/2;
  33.         while( j >= k)
  34.         {
  35.             j -= k;
  36.             k /= 2;
  37.         }
  38.         if(j < k)j += k;
  39.     }
  40. }
  41. void fft(Complex* y,int len,int on)
  42. {
  43.     change(y,len);
  44.     for(int h = 2;h <= len;h <<= 1)
  45.     {
  46.         Complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
  47.         for(int j = 0;j < len;j += h)
  48.         {
  49.             Complex w(1,0);
  50.             for(int k = j;k < j+h/2;k++)
  51.             {
  52.                 Complex u = y[k];
  53.                 Complex t = w*y[k+h/2];
  54.                 y[k] = u+t;
  55.                 y[k+h/2] = u-t;
  56.                 w = w*wn;
  57.             }
  58.         }
  59.     }
  60.     if(on == -1)
  61.         for(int i = 0;i < len;i++)
  62.             y[i].r /= len;
  63. }
  64. Complex x1[N<<2];
  65. Complex x2[N<<2];
  66. int n,m,a[N],b[N];
  67. int num[N<<1]; 
  68. int main(void){
  69.     scanf("%d%d",&n,&m);
  70.     for(int i=0;i<=n;i++)
  71.         scanf("%d",&a[i]);
  72.     for(int i=0;i<=m;i++)
  73.         scanf("%d",&b[i]);
  74.     int len,len1;
  75.     //len1=n+m+1;
  76.     len=1;
  77.     while(len < ((n+1)<<1) || len < ((m+1)<<1)) len <<= 1;
  78.     for(int i = 0; i <= n; i++)
  79.        x1[i] = Complex(a[i],0);
  80.     for(int i = n+1; i < len; i++)
  81.        x1[i] = Complex(0,0);
  82.     for(int i = 0; i <= m; i++)
  83.        x2[i] = Complex(b[i],0);
  84.     for(int i = m+1; i < len; i++)
  85.        x2[i] = Complex(0,0);
  86.     fft(x1,len,1);
  87.     fft(x2,len,1);
  88.     for(int i = 0;i < len;i++)
  89.             x1[i] = (x1[i]*x2[i]);
  90.     fft(x1,len,-1);    
  91.     for(int i = 0;i <= n+m;i++)
  92.         num[i] = (x1[i].r+0.5);    
  93.     for(int i=0;i<=n+m;i++)
  94.         printf("%d%c",num[i],i==n+m?'\n':' ');
  96.     return 0;    
  97. }

FFT板子

题目链接：https://www.luogu.com.cn/problem/P1919

递归版

  2. #include<bits/stdc++.h> 
  3. using namespace std;
  4. const double pi = acos(-1);
  5. const int N = 3e6+5;
  6. int ans[N];
  7. struct Complex{
  8.     double x,y;
  9.     Complex(double x = 0,double y = 0):x(x),y(y) { }
  10. }A[N],B[N];
  11. Complex operator * (Complex X,Complex Y)
  12. {
  13.     return Complex(X.x*Y.x-X.y*Y.y,X.x*Y.y+X.y*Y.x);
  14. }
  15. Complex operator + (Complex X,Complex Y)
  16. {
  17.     return Complex(X.x+Y.x,X.y+Y.y);
  18. }
  19. Complex operator - (Complex X,Complex Y)
  20. {
  21.     return Complex(X.x-Y.x,X.y-Y.y);
  22. }
  23. void FFT(Complex *a,int n,int flag)
  24. {
  25.     if(n==1)
  26.         return ;
  27.     Complex a1[n>>1],a2[n>>1];
  28.     for (int i=0;i<=n;i+=2)
  29.         a1[i>>1] = a[i],a2[i>>1] = a[i+1];
  30.     FFT(a1,n>>1,flag);
  31.     FFT(a2,n>>1,flag);
  32.     Complex wn = Complex(cos(2*pi/n),flag*sin(2*pi/n)),w = Complex(1,0);
  33.     for (int i=0;i<(n>>1);i++,w=w*wn)
  34.     {
  35.         a[i] = a1[i]+w*a2[i];
  36.         a[i+(n>>1)] = a1[i]-w*a2[i];
  37.     }
  38. }
  39. int main ()
  40. {
  41.     string s1,s2;
  42.     cin>>s1>>s2;
  43.     int l1 = s1.size(),l2 = s2.size();
  44.     for (int i=0;i<l1;i++)
  45.         A[i] = Complex(s1[l1-i-1]-'0',0);
  46.     for (int i=0;i<l2;i++)
  47.         B[i] = Complex(s2[l2-i-1]-'0',0);
  49.     int n = 1;
  50.     while(n<l1+l2-1)n<<=1;
  52.     FFT(A,n,1);
  53.     FFT(B,n,1);
  55.     for (int i=0;i<=n;i++)
  56.         A[i] = A[i]*B[i];
  58.     FFT(A,n,-1);
  60.     for (int i=0;i<n;i++)
  61.     {
  62.         ans[i]+=A[i].x/n+0.5;
  63.         ans[i+1] += ans[i]/10;
  64.         ans[i]%=10;
  65.     }
  66.     while(!ans[n]&&n>=0)
  67.         n--;
  68.     if(n==-1)
  69.         puts("0");
  70.     else
  71.         for (int i=n;i>=0;i--)
  72.             cout<<ans[i];
  73.     return 0;
  74. }

迭代版

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int N = 3e6+5;
  4. const double pi = acos(-1);
  5. struct Complex{
  6.     double x,y;
  7.     Complex(double x1=0,double y1=0){
  8.         x = x1, y = y1;
  9.     }
  10.     Complex operator *(const Complex& C) const{
  11.         return Complex(x*C.x-y*C.y,x*C.y+y*C.x);
  12.     }
  13.     Complex operator +(const Complex& C) const{
  14.         return Complex(x+C.x,y+C.y);
  15.     }
  16.     Complex operator -(const Complex& C) const{
  17.         return Complex(x-C.x,y-C.y);
  18.     }
  19. }a[N],b[N];
  20. int ans[N],rev[N];
  21. void FFT(Complex *a,int n,int flag)
  22. {
  23.     for (int i=0;i<n;i++)
  24.         if(i<rev[i])
  25.             swap(a[i],a[rev[i]]);
  27.     for (int mid=1;mid<n;mid<<=1)
  28.     {
  29.         Complex wn = Complex(cos(pi/mid),flag*sin(pi/mid));
  30.         for (int len=mid<<1,pos=0;pos<n;pos+=len)
  31.         {
  32.             Complex w = Complex(1,0);
  33.             for (int k=0;k<mid;k++,w=w*wn)
  34.             {
  35.                 Complex x = a[k+pos];
  36.                 Complex y = w*a[k+pos+mid];
  37.                 a[k+pos] = x+y;
  38.                 a[k+pos+mid] = x-y;
  39.             }
  40.         }
  41.     }
  43.     if(flag==-1)
  44.         for (int i=0;i<n;i++)
  45.             a[i].x/=n;
  46. }
  47. int main ()
  48. {
  49.     string s1,s2;
  50.     cin>>s1>>s2;
  51.     int l1 = s1.size(),l2 = s2.size();
  52.     for (int i=0;i<l1;i++)
  53.         a[i] = Complex(s1[l1-i-1]-'0',0);
  54.     for (int i=0;i<l2;i++)
  55.         b[i] = Complex(s2[l2-i-1]-'0',0);
  57.     int n=1,l=0;
  58.     while(n<l1+l2-1)n<<=1,l++;
  60.     for (int i=0;i<n;i++)
  61.         rev[i] = (rev[i>>1]>>1)|((i&1)<<(l-1));
  63.     FFT(a,n,1);
  64.     FFT(b,n,1);
  66.     for (int i=0;i<n;i++)
  67.         a[i] = a[i]*b[i];
  69.     FFT(a,n,-1);
  71.     for (int i=0;i<n;i++)
  72.     {
  73.         ans[i] += a[i].x+0.5;
  74.         ans[i+1] += ans[i]/10;
  75.         ans[i] %= 10;
  76.     }
  78.     while(!ans[n]&&~n)n--;
  79.     if(n==-1)
  80.         puts("0") ;
  81.     else
  82.     {
  83.         for (int i=n;i>=0;i--)
  84.             cout<<ans[i];
  85.     }
  86.     return 0;
  87. }

三步变两步优化

image.png

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. const int N = 3e6+5;
  4. const double pi = acos(-1);
  5. struct Complex{
  6.     double x,y;
  7.     Complex(double x1=0,double y1=0){
  8.         x = x1, y = y1;
  9.     }
  10.     Complex operator *(const Complex& C) const{
  11.         return Complex(x*C.x-y*C.y,x*C.y+y*C.x);
  12.     }
  13.     Complex operator +(const Complex& C) const{
  14.         return Complex(x+C.x,y+C.y);
  15.     }
  16.     Complex operator -(const Complex& C) const{
  17.         return Complex(x-C.x,y-C.y);
  18.     }
  19. }a[N],b[N];
  20. int ans[N],rev[N];
  21. void FFT(Complex *a,int n,int flag)
  22. {
  23.     for (int i=0;i<n;i++)
  24.         if(i<rev[i])
  25.             swap(a[i],a[rev[i]]);
  27.     for (int mid=1;mid<n;mid<<=1)
  28.     {
  29.         Complex wn = Complex(cos(pi/mid),flag*sin(pi/mid));
  30.         for (int len=mid<<1,pos=0;pos<n;pos+=len)
  31.         {
  32.             Complex w = Complex(1,0);
  33.             for (int k=0;k<mid;k++,w=w*wn)
  34.             {
  35.                 Complex x = a[k+pos];
  36.                 Complex y = w*a[k+pos+mid];
  37.                 a[k+pos] = x+y;
  38.                 a[k+pos+mid] = x-y;
  39.             }
  40.         }
  41.     }
  43.     if(flag==-1)
  44.         for (int i=0;i<n;i++)
  45.             a[i].x/=n,a[i].y/=n;//优化的变化
  46. }
  47. int main ()
  48. {
  49.     string s1,s2;
  50.     cin>>s1>>s2;
  51.     int l1 = s1.size(),l2 = s2.size();
  52.     for (int i=0;i<l1;i++)
  53.         a[i].x = s1[l1-i-1]-'0';
  54.     for (int i=0;i<l2;i++)
  55.         a[i].y = s2[l2-i-1]-'0';
  57.     int n=1,l=0;
  58.     while(n<l1+l2-1)n<<=1,l++;
  60.     for (int i=0;i<n;i++)
  61.         rev[i] = (rev[i>>1]>>1)|((i&1)<<(l-1));
  63.     FFT(a,n,1);//只需要一次FFT
  65.     for (int i=0;i<n;i++)
  66.         a[i] = a[i]*a[i];
  68.     FFT(a,n,-1);
  70.     for (int i=0;i<n;i++)
  71.     {
  72.         ans[i] += a[i].y/2+0.5;//取出虚数除以2
  73.         ans[i+1] += ans[i]/10;
  74.         ans[i] %= 10;
  75.     }
  77.     while(!ans[n]&&~n)n--;
  78.     if(n==-1)
  79.         puts("0") ;
  80.     else
  81.     {
  82.         for (int i=n;i>=0;i--)
  83.             cout<<ans[i];
  84.     }
  85.     return 0;
  86. }

最详细的博客链接：
https://fanfansann.blog.csdn.net/article/details/111710443
刷过FFT的题目：
https://www.luogu.com.cn/problem/P1919
https://www.luogu.com.cn/problem/P3803
https://ac.nowcoder.com/acm/contest/11166/H
AC代码：

  1. /*
  2. H题：Hash Function
  3. 标签：简单数论，卷积，FFT/NTT 
  4. */
  5. #include<bits/stdc++.h>
  6. using namespace std;
  7. const int N = 5e5+5, maxn = 1<<20;
  8. const double pi = acos(-1);
  9. struct Complex{
  10.     double x,y;
  11.     Complex(double x1=0,double y1=0){
  12.         x = x1, y = y1;
  13.     }
  14.     Complex operator * (const Complex &C) {
  15.         return Complex(x*C.x-y*C.y,x*C.y+y*C.x);
  16.     }
  17.     Complex operator + (const Complex &C) {
  18.         return Complex(x+C.x,y+C.y);
  19.     }
  20.     Complex operator - (const Complex &C) {
  21.         return Complex(x-C.x,y-C.y);
  22.     }
  23. }a[maxn],b[maxn];
  24. bool s[maxn];
  25. int rev[maxn];
  26. void FFT(Complex *a,int n,int flag)
  27. {
  28.     for (int i=0;i<n;i++)
  29.         if(i<rev[i])
  30.             swap(a[i],a[rev[i]]);
  32.     for (int mid=1;mid<n;mid<<=1)
  33.     {
  34.         Complex wn = Complex(cos(pi/mid),flag*sin(pi/mid));
  35.         for (int len=mid<<1,pos=0;pos<n;pos+=len)
  36.         {
  37.             Complex w = Complex(1,0);
  38.             for (int k=0;k<mid;k++,w=w*wn)
  39.             {
  40.                 Complex x = a[k+pos], y = w*a[k+pos+mid];
  41.                 a[k+pos] = x+y;
  42.                 a[k+pos+mid] = x-y;
  43.             }
  44.         }
  45.     }
  47.     if(flag==-1)
  48.         for (int i=0;i<n;i++)
  49.             a[i].x/=n;
  50. }
  51. int main ()
  52. {
  53.     int n;
  54.     scanf("%d",&n);
  55.     for (int i=1;i<=n;i++)
  56.     {
  57.         int x;
  58.         scanf("%d",&x);
  59.         a[x].x = 1;
  60.         b[N-x].x = 1;
  61.     }
  62.     for (int i=0;i<maxn;i++)
  63.         rev[i] = (rev[i>>1]>>1)|((i&1)<<19);
  65.     FFT(a,maxn,1);
  66.     FFT(b,maxn,1);
  68.     for (int i=0;i<maxn;i++)
  69.         a[i] = a[i]*b[i];
  70.     FFT(a,maxn,-1);
  71.     for (int i=0;i<maxn;i++)
  72.     {
  73.         int x = a[i].x+0.5;
  74.         if(x>0)
  75.             s[abs(N-i)] = 1;
  76.     }
  77.     for (int i=n;i<N;i++)
  78.     {
  79.         int f = 1;
  80.         for (int j=i;j<N;j+=i)
  81.             if(s[j])
  82.             {
  83.                 f=0;
  84.                 break;
  85.             }
  86.         if(f)
  87.         {
  88.             printf("%d",i);
  89.             break;
  90.         }
  91.     }
  92.     return 0;
  93. }