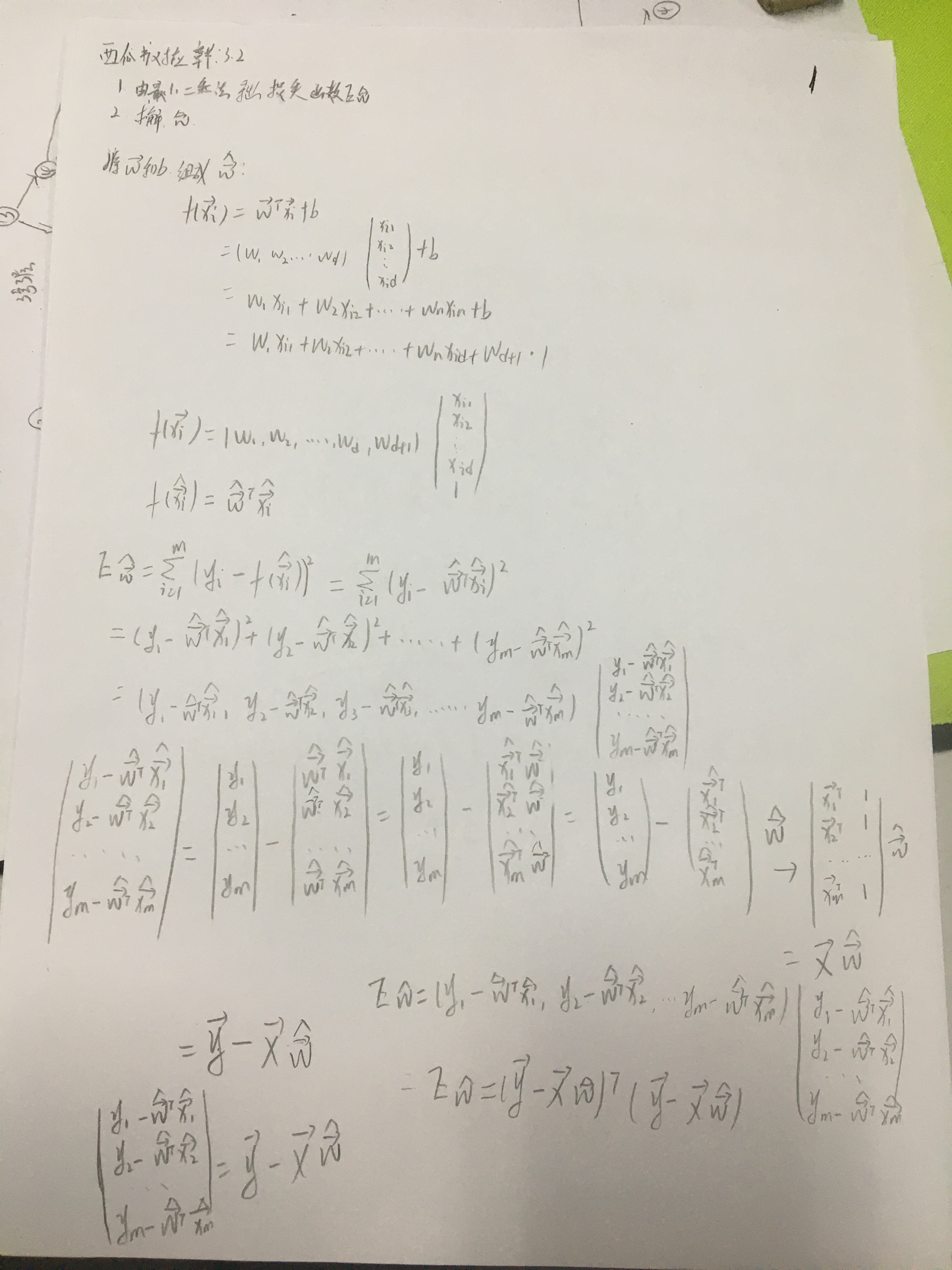一元线性回归
首先第1,2节是讲的基本形式,线性回归
它主要包含三个方面:
- 算法原理
- 线性回归的最小二乘估计和最大似然估计
- 求解和
算法原理
通过一个例子来论证,发际线高度和计算机水平之间的关系
采样一批点,沿着一条直线有上有下,不是用曲线穿起来,而是用一条直线串过去。如果穿起来,我们采集的数据有误差,这时候就把误差也考虑进去了。
这里有个知识点
- 正交回归: 点到直线的距离
- 线性回归: 点到点的距离
仅通过发际线来预测计算机水平:
二值离散特征,例子:颜值 (0: 好看, 1: 非常好看):
有序的多值离散特征:健康程度(0:健康,1:很健康,2:特别健康)
无序的多值离散特征: 肤色(黄色(1,0,0), 白色(0,1,0), 黑色(0,0,1))
最小二乘估计
基于均方误差最小化来进行模型求解的方法称为最小二乘法
极大似然估计
用途: 估计概率分布的参数值
方法: 对于离散型(连续型)随机变量,假设其概率质量函数为(概率密度函数为),其中 为待估计的参数值(可以有多个),现有是来自的n个独立同分布的样本,它们的联合概率为
其中是已知量, 为未知量,因此以上概率是一个关于的函数,称为样本的似然函数。极大似然估计的直观想法:使得观测样本出现概率最大的分布就是待求分布,也即使得联合概率(似然函数)取得最大值的即为的估计量。
举个例子:
有一批观测数据,我们假设它服从正态分布,其中为待估计的参数值,怎么用极大似然估计求出呢?
总体上分为三步
第一步:写出随机变量的概率密度函数
第二步: 写出似然函数
第三步:求出使得取得最大值的
对于对数函数是单调递增函数,所以和有相同的最大值点,而且用对数函数性质能简化的连乘项,所以我们通常会用来代替来求,加了对数函数符号的似然函数称为对数似然函数。
对于线性回归来说,可以假设下面的模型
为不受控制的随机误差,通常假设其均值为0的正态分布(高斯提出的,也可以用中心极限定理解释),所以的概率密度函数为
若将用等价替换可得
这里多少有点问题,应该感觉不对。y随x变化而变化,所以每次都是不同的
我们可以看作,下面可以使用极大似然估计来估计和的值,似然函数为
其中都是常数,所以最小化等价于最小化,也就是
这个公式也就是公式3.4,等价于最小二乘法。
求解和其本质是一个多元函数求最值点的问题,更具体的是凸函数求最值的问题。
思路:
- 证明是关于和的凸函数
- 用凸函数求最值的思路求解和
凸集: 设集合,对于任意与任意的,有
则称为凸集。凸集的集合意义: 若两个点属于此集合,则两点连线上的任意一点均属于此集合。常见的凸集有空集,维欧氏空间
凸函数: 设是非空凸集, 是定义在上的函数,如果对任意的,均有
则称为上的凸函数。
梯度(多元函数的一阶导数): 设元函数对自变量的各个分量的偏导数都存在,则称函数在处一阶可导数,并称向量
为函数在处的一阶导数或者梯度。
Hessian(海塞)矩阵(多元函数的二阶导数): 设元函数对自变量的各分量的二阶偏导数都存在,则称函数在处一阶可导数,并称矩阵
为函数在处的二阶导数或Hessia(海塞)矩阵。
定理: 设是非空开空集, , 且在上二阶连续可微,如果的Hessian(海塞)矩阵在上是半正定的,则在上的凸函数。这里类比一元函数判断凹凸性。
因此,只需要证明的Hessian(海塞)矩阵
是正定的,那么就是关于和的凸函数。
接下来求的一阶偏导
不会公式对齐。。。
机器学习三要素: