10.6.1 Adelson-Velskii-Landi 树（ AVL 树）

AVL树是一种自平衡树。添加或移除节点时， AVL树会尝试保持自平衡。任意一个节点（不论深度）的左子树和右子树高度最多相差 1。添加或移除节点时， AVL树会尽可能尝试转换为完全树。从创建我们的 AVLTree 类开始，声明如下。

class AVLTree extends BinarySearchTree {
  constructor(compareFn = defaultCompare) {
    super(compareFn);
    this.compareFn = compareFn;
    this.root = null;
  }
}

既然 AVL 树是一个 BST，我们可以扩展我们写的 BST 类，只需要覆盖用来维持 AVL 树平衡的方法，也就是 insert、 insertNode 和 removeNode 方法。所有其他的 BST 方法将会被 AVLTree 类继承。

在 AVL 树中插入或移除节点和 BST 完全相同。然而， AVL 树的不同之处在于我们需要检验它的平衡因子，如果有需要，会将其逻辑应用于树的自平衡。

我们将会学习怎样创建 remove 和 insert 方法，但是首先需要学习 AVL 树的术语和它的旋转操作。

1. 节点的高度和平衡因子

正如本章开头所述，节点的高度是从节点到其任意子节点的边的最大值。下图展示了一个包含每个节点高度的树。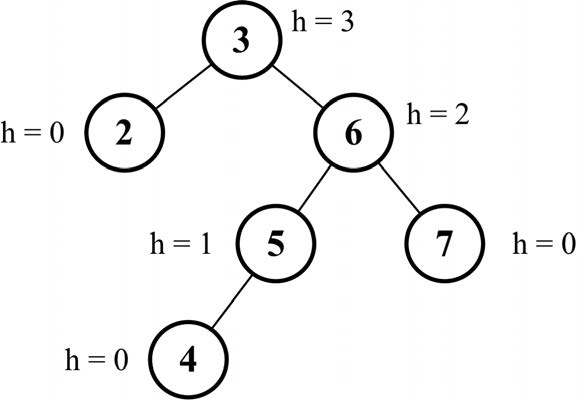

计算一个节点高度的代码如下。

getNodeHeight(node) {
  if (node == null) {
    return -1;
  }
  return (
    Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1
  );
}

在 AVL 树中，需要对每个节点计算右子树高度（ hr）和左子树高度（ hl）之间的差值，该
值（ hr－ hl）应为 0、 1 或1。如果结果不是这三个值之一，则需要平衡该 AVL 树。这就是平衡
因子的概念。

下图举例说明了一些树的平衡因子（所有的树都是平衡的）。

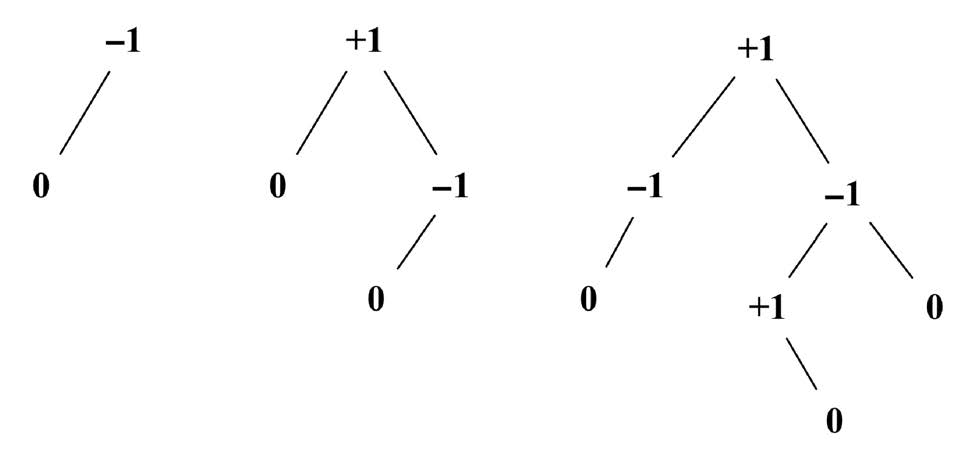
遵循计算一个节点的平衡因子并返回其值的代码如下。

getBalanceFactor(node) {
  const heightDifference =
    this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
  switch (heightDifference) {
    case -2:
      return BalanceFactor.UNBALANCED_RIGHT;
    case -1:
      return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
    case 1:
      return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
    case 2:
      return BalanceFactor.UNBALANCED_LEFT;
    default:
      return BalanceFactor.BALANCED;
  }
}

为了避免直接在代码中处理平衡因子的数值，我们还要创建一个用来作为计数器的 JavaScript 常量。

const BalanceFactor = {
  UNBALANCED_RIGHT: 1,
  SLIGHTLY_UNBALANCED_RIGHT: 2,
  BALANCED: 3,
  SLIGHTLY_UNBALANCED_LEFT: 4,
  UNBALANCED_LEFT: 5,
};

我们会在下面学习到每个 heightDifference 表示什么。

2. 平衡操作——AVL 旋转

在对 AVL 树添加或移除节点后，我们要计算节点的高度并验证树是否需要进行平衡。向 AVL 树插入节点时，可以执行单旋转或双旋转两种平衡操作，分别对应四种场景。

左-左（ LL）：向右的单旋转
右-右（ RR）：向左的单旋转
左-右（ LR）：向右的双旋转（先 RR 旋转，再 LL 旋转）
右-左（ RL）：向左的双旋转（先 LL 旋转，再 RR 旋转）

• 左-左（ LL）：向右的单旋转
  这种情况出现于节点的左侧子节点的高度大于右侧子节点的高度时，并且左侧子节点也是平衡或左侧较重的，如下图所示。

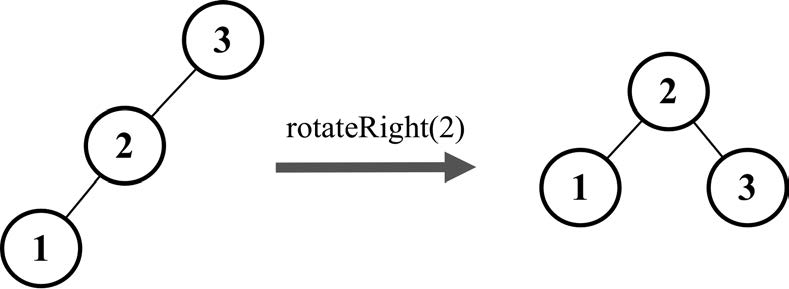
我们来看一个实际的例子，如下图所示。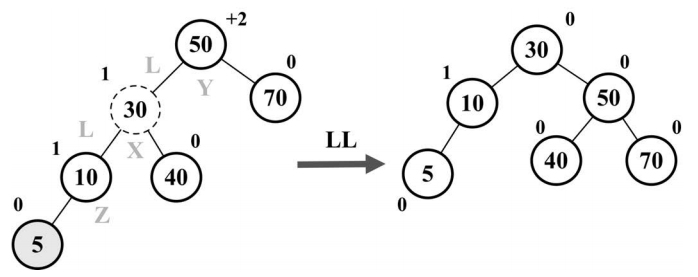

假设向 AVL 树插入节点 5，这会造成树失衡（节点 50-Y 高度为+2），需要恢复树的平衡。下面是我们执行的操作：
（1）与平衡操作相关的节点有三个（ X、 Y、 Z），将节点 X 置于节点 Y（平衡因子为+2）所在
的位置（行 {1}）；
（2）节点 X 的左子树保持不变
（3）将节点 Y 的左子节点置为节点 X 的右子节点（行 {2}）；
（4）将节点 X 的右子节点置为节点 Y（行 {3}）。

下面的代码举例说明了整个过程。

rotationLL(node) {
  const tmp = node.left; // {1}
  node.left = tmp.right; // {2}
  tmp.right = node; // {3}
  return tmp;
}

• 右-右（ RR）：向左的单旋转

右-右的情况和左-左的情况相反。它出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点也是平衡或右侧较重的，如下图所示。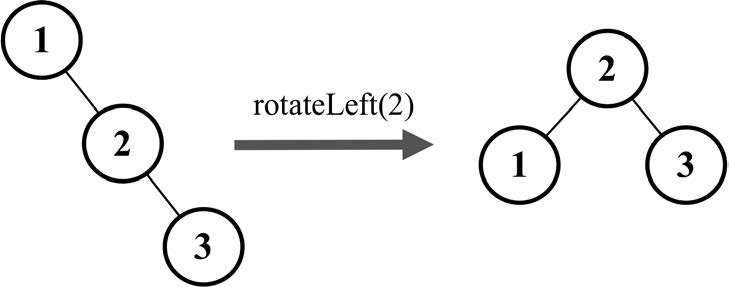

我们来看一个实际的例子，如下图所示。


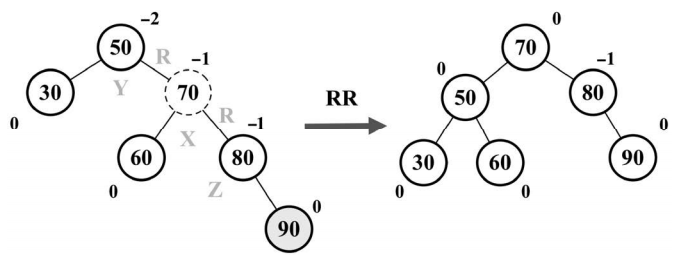
假设向 AVL 树插入节点 90，这会造成树失衡（节点 50-Y 高度为2），因此需要恢复树的平衡。下面是我们执行的操作：
(1)与平衡操作相关的节点有三个（ X、 Y、 Z），将节点 X 置于节点 Y（平衡因子为2）所在
的位置（行{1}）；
(2)节点 X 的右子树保持不变；
(3)将节点 Y 的右子节点置为节点 X 的左子节点（行{2}）；
(4)将节点 X 的左子节点置为节点 Y（行{3}）。

下面的代码举例说明了整个过程。

rotationRR(node) {
  const tmp = node.right; // {1}
  node.right = tmp.left; // {2}
  tmp.left = node; // {3}
  return tmp;
}

• 左-右（LR）：向右的双旋转.

这种情况出现于左侧子节点的高度大于右侧子节点的高度，并且左侧子节点右侧较重。在这种情况下，我们可以对左侧子节点进行左旋转来修复，这样会形成左-左的情况，然后再对不平衡的节点进行一个右旋转来修复，如下图所示。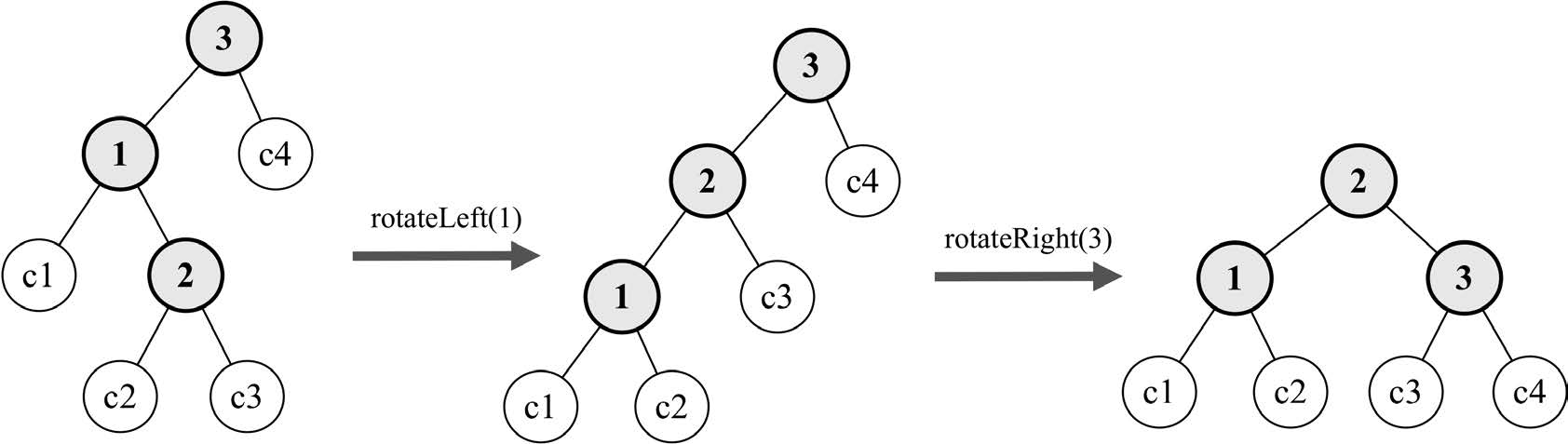

我们来看一个实际的例子，如下图所示

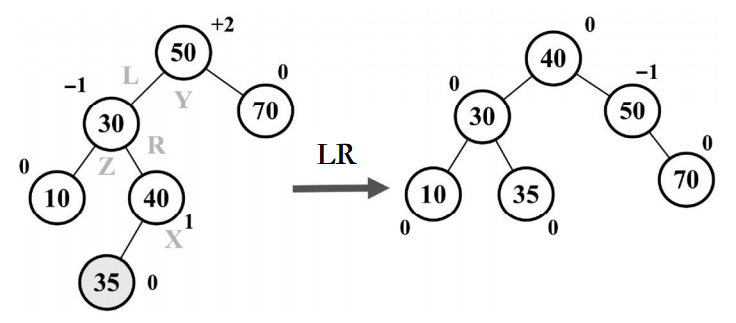
假设向 AVL 树插入节点 35，这会造成树失衡（节点 50-Y 高度为+2），需要恢复树的平衡。下面是我们执行的操作：
(1)将节点 X 置于节点 Y（平衡因子为+2）所在的位置；
(2)将节点 Y 的左子节点置为节点 X 的右子节点；
(3)将节点 Z 的右子节点置为节点 X 的左子节点；
(4)将节点 X 的右子节点置为节点 Y；
(5)将节点 X 的右子节点置为节点 Z。

基本上，就是先做一次 RR 旋转（左旋），再做一次 LL 旋转（右旋）。

下面的代码举例说明了整个过程。

rotationLR(node) {
  node.left = this.rotationRR(node.left);
  return this.rotationLL(node);
}

• 右-左（RL）：向左的双旋转

右-左的情况和左-右的情况相反。这种情况出现于右侧子节点的高度大于左侧子节点的高度，并且右侧子节点左侧较重。在这种情况下我们可以对右侧子节点进行右旋转来修复，这样会形成右右的情况，然后我们再对不平衡的节点进行一个左旋转来修复，如下图所示。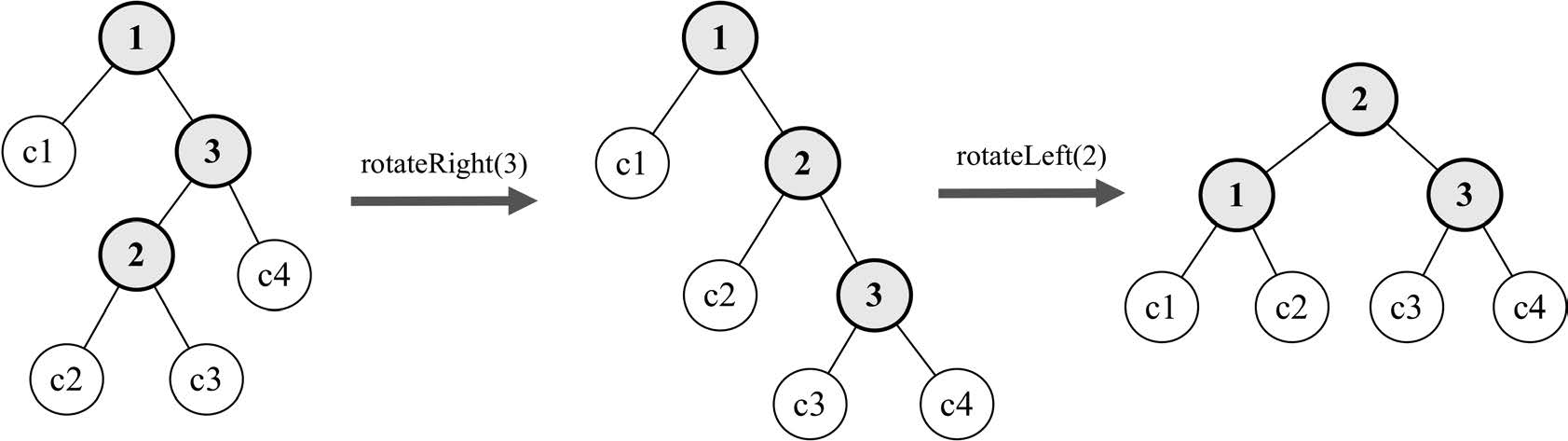

我们来看一个实际的例子，如下图所示。

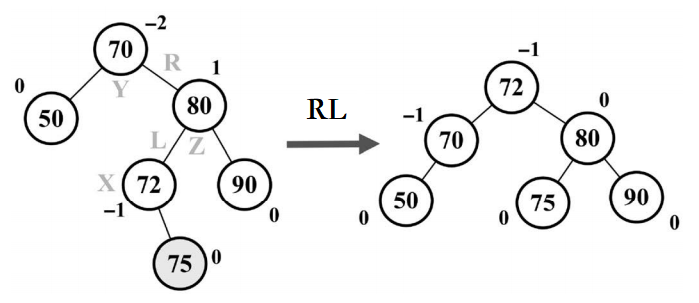
假设向 AVL 树插入节点 75，这会造成树失衡（节点 70-Y 高度为2），需要恢复树的平衡。
下面是我们执行的操作：
（1）将节点 X 置于节点 Y（平衡因子为2）所在的位置；
（2）将节点 Z 的左子节点置为节点 X 的右子节点；
（3）将节点 Y 的右子节点置为节点 X 的左子节点 ;
（4）将节点 X 的左子节点置为节点 Y ;
（5）将节点 X 的右子节点置为节点 Z。

基本上，就是先做一次 LL 旋转（右旋），再做一次 RR 旋转（左旋）。

下面的代码举例说明了整个过程。

rotationRL(node) {
    node.right = this.rotationLL(node.right);
    return this.rotationRR(node);
}

理解了这些概念，我们就可以专注于向树添加阶段和从树移除节点的代码了。

3. 向 AVL 树插入节点

向 AVL 树插入节点和在 BST 中是一样的。除了插入节点外，我们还要验证插入后树是否还是平衡的，如果不是，就要进行必要的旋转操作。

下面的代码向 AVL 树插入了一个新节点。

function insert(key) {
  this.root = this.insertNode(this.root, key);
}

function insertNode(node, key) {
  // 像在 BST 树中一样插入节点
  if (node == null) {
    return new Node(key);
  } else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
    node.left = this.insertNode(node.left, key);
  } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
    node.right = this.insertNode(node.right, key);
  } else {
    return node; // 重复的键
  }
  // 如果需要，将树进行平衡操作
  const balanceFactor = this.getBalanceFactor(node); // {1}
  if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
    // {2}
    if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {
      // {3}
      node = this.rotationLL(node); // {4}
    } else {
      return this.rotationLR(node); // {5}
    }
  }
  if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
    // {6}
    if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {
      // {7}
      node = this.rotationRR(node); // {8}
    } else {
      return this.rotationRL(node); // {9}
    }
  }
  return node;
}

在向 AVL 树插入节点后，我们需要检查树是否需要进行平衡，因此要使用递归计算以每个插入树的节点为根的节点的平衡因子（行{1}），然后对每种情况应用正确的旋转。

如果在向左侧子树插入节点后树不平衡了（行{2}），我们需要比较是否插入的键小于左侧子节点的键（行{3}）。如果是，我们要进行 LL 旋转（行{4}）。否则，要进行 LR 旋转（行{5}）。

如果在向右侧子树插入节点后树不平衡了（行{6}），我们需要比较是否插入的键小于右侧子节点的键（行{7}）。如果是，我们要进行 RR 旋转（行{8}）。否则，要进行 RL 旋转（行{9}）。 

4. 从 AVL 树中移除节点

从 AVL 树移除节点和在 BST 中是一样的。除了移除节点外，我们还要验证移除后树是否还是平衡的，如果不是，就要进行必要的旋转操作。

下面的代码从 AVL 树移除了一个节点。

function removeNode(node, key) {
  node = super.removeNode(node, key); // {1}
  if (node == null) {
    return node; // null，不需要进行平衡
  }
  // 检测树是否平衡
  const balanceFactor = this.getBalanceFactor(node); // {2}
  if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
    // {3}
    const balanceFactorLeft = this.getBalanceFactor(node.left); // {4}
    if (
      balanceFactorLeft === BalanceFactor.BALANCED ||
      balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
    ) {
      // {5}
      return this.rotationLL(node); // {6}
    }
    if (balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT) {
      // {7}
      return this.rotationLR(node.left); // {8}
    }
  }
  if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
    // {9}
    const balanceFactorRight = this.getBalanceFactor(node.right); // {10}
    if (
      balanceFactorRight === BalanceFactor.BALANCED ||
      balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
    ) {
      // {11}
      return this.rotationRR(node); // {12}
    }
    if (balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT) {
      // {13}
      return this.rotationRL(node.right); // {14}
    }
  }
  return node;
}

既然 AVLTree 类是 BinarySearchTree 类的子类，我们也可以使用 BST 的 removeNode方法来从 AVL 树中移除节点（行{1}）。在从 AVL 树中移除节点后，我们需要检查树是否需要进行平衡，所以使用递归计算以每个移除的节点为根的节点的平衡因子（行{2}），然后需要对每种情况应用正确的旋转。

如果在从左侧子树移除节点后树不平衡了（行{3}），我们要计算左侧子树的平衡因子（行{4}）。如果左侧子树向左不平衡（行{5}），要进行 LL 旋转（行{6}）；如果左侧子树向右不平衡（行{7}），要进行 LR 旋转（行{8}）。

最后一种情况是，如果在从右侧子树移除节点后树不平衡了（行{9}），我们要计算右侧子树的平衡因子（行{10}）。如果右侧子树向右不平衡（行{11}），要进行 RR 旋转（行{12}）；如果右侧子树向左不平衡（行{13}），要进行 LR 旋转（行{14}）。