一、梯度下降

1、何为和为何？

梯度下降是求解机器学习算法的的模型参数时最常用的方法之一：

梯度下降用于求解损失函数的最小值，那么如果我们想求解损失函数的最大值，那么就需要用到梯度上升函数。（这个以后详谈，先挖坑）

在机器学习中，梯度下降法发展成了两种梯度下降的方法——分别为随机梯度下降法，与批量梯度下降法。
目前我们需要解决的问题是 随机梯度下降法。

2、如何理解梯度下降？

我们可以先从一个简单的例子中开始讲解：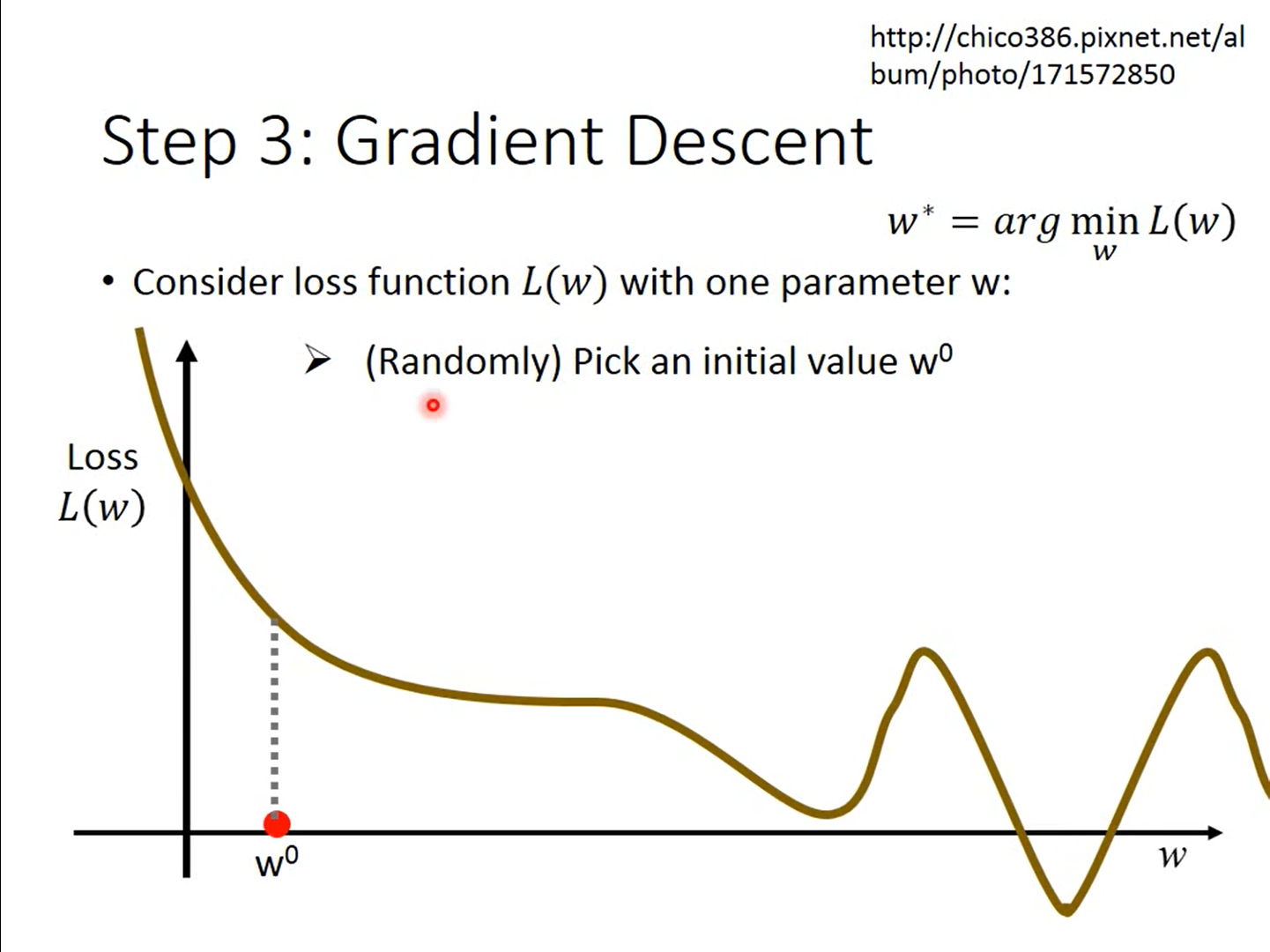

图1 与的关系

(随机梯度下降算法)首先随机选择一个点，求导计算该点的梯度（即导数。）

我们发现我们随机找的点，大概率下并不是在局部最优(local minimum)或者全局最优解(gobal minimum)，因此我们需要接着找，假设我们跟着图来，如何找到更小的解呢？显然往右(w值增加)
那么我们有：

我们先思考一下现在的导数（斜率）为负数，即左边高，右边低，如果我们要找最小值，那么值就要增加，而我们已知：已经小于0，那实际上就是在向右移动。
相应的，如果的导数为正数，即右边高，左边低，那么我们一样可以：已经大于0，那实际上就是在向左移动。
而这个我们称之为学习率！
李宏毅老师的说法是：
学习率越大，那么他在跨出下一步的时候就会越大，那么我们可以得到以下的结论：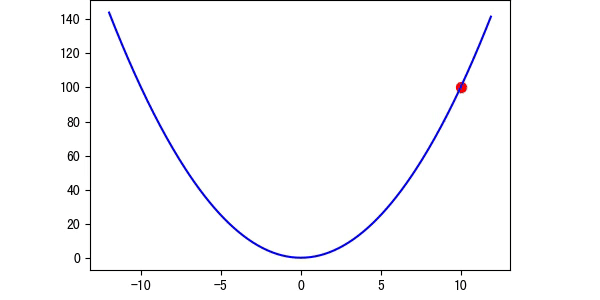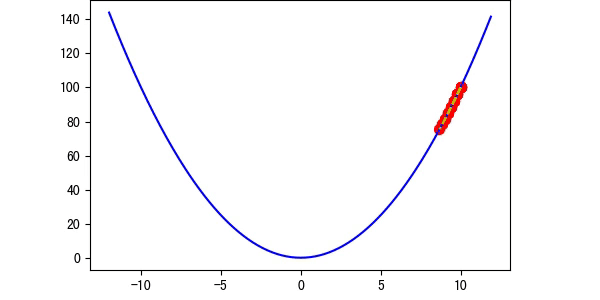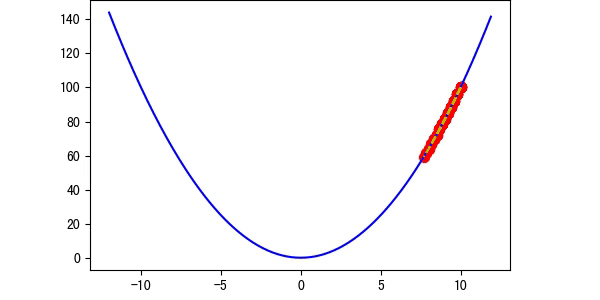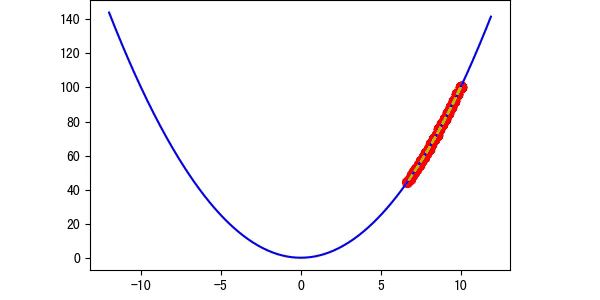

图2 学习率过小

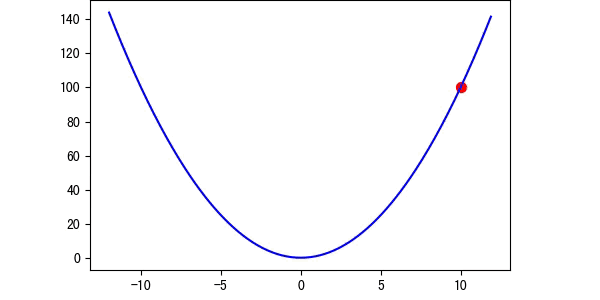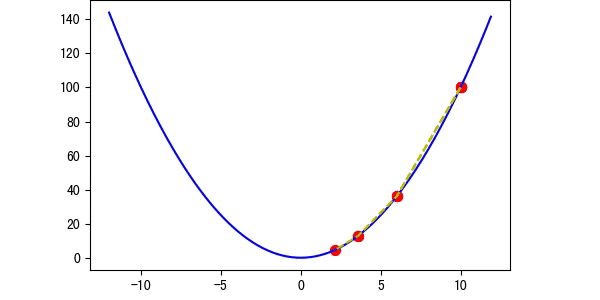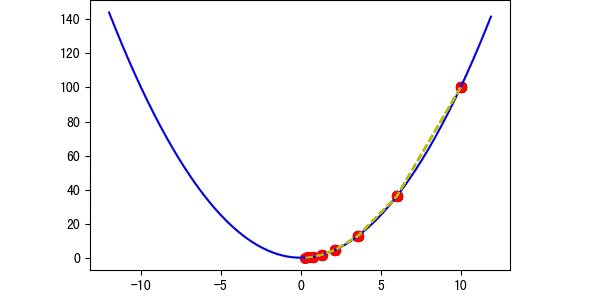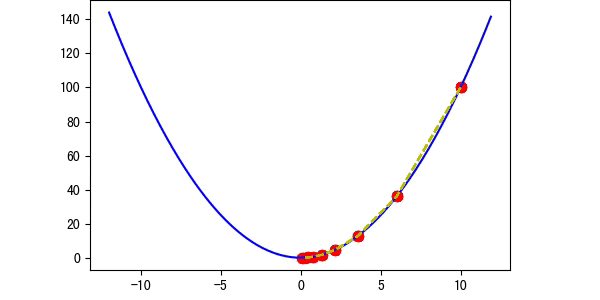
图3 学习率适中

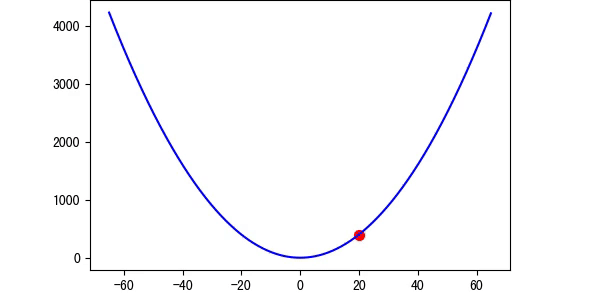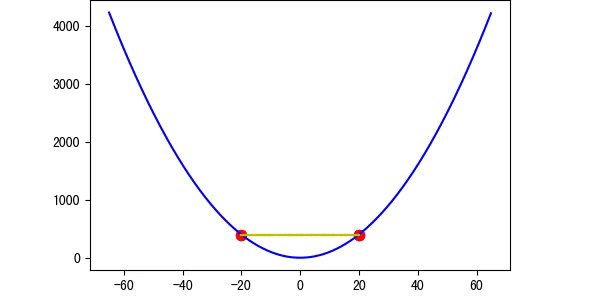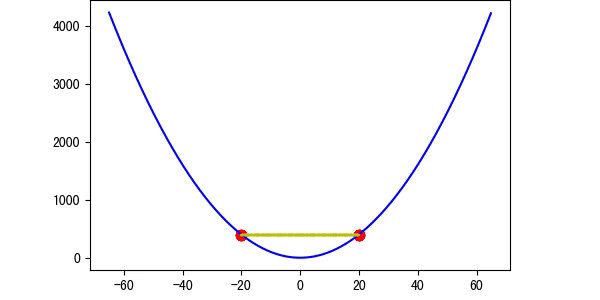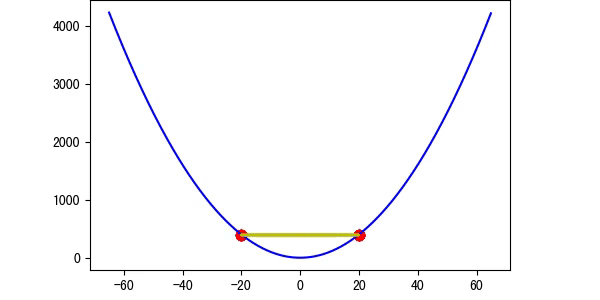
图4 学习率等于1(图中是特殊情况，正好对称)

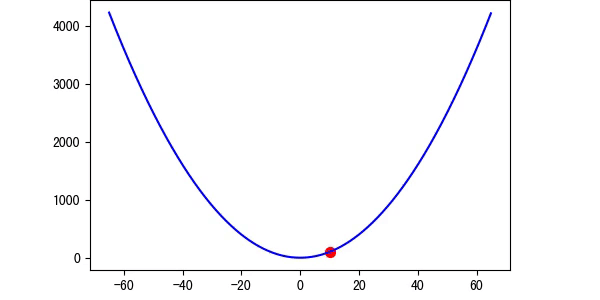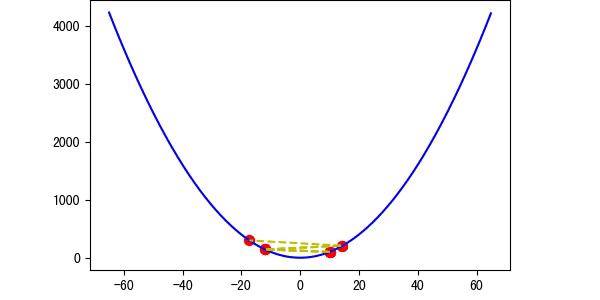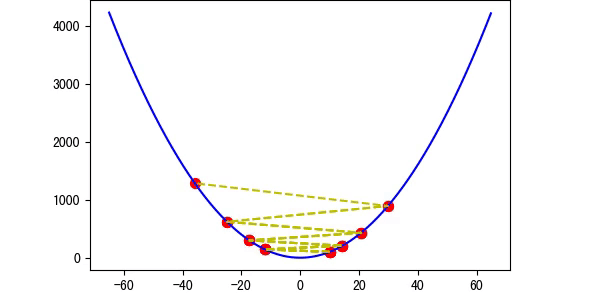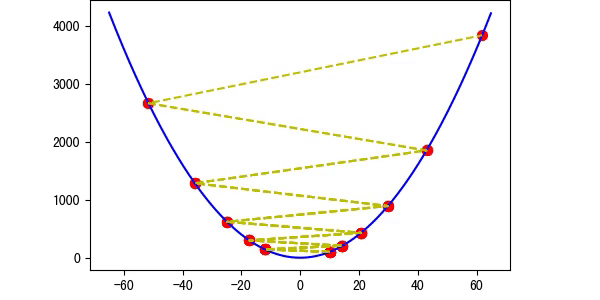
图5 存在概率越过最优解

因此学习率的选择至关重要（现在的我还不知道如何通过代码让其自动选择学习率）

在计算的时候我们首先明确一点我们现在做的是梯度下降（即找到当前函数的最小值）

自动调节学习率的方法(自行适应梯度算法)

我们有一个可以让学习率自动下降的方法，就是让学习率等于一个函数，例如:（t是每次的执行的次数）



首先就是均方根，根据百度百科的解释：
将所有值平方求和，求其均值，再开平方，就得到均方根值、
就是在中的梯度。
然后我们可以得到：
与可以约掉一个，那么我们可以得到：

分母就是为了造成反差，让异常值显示出来：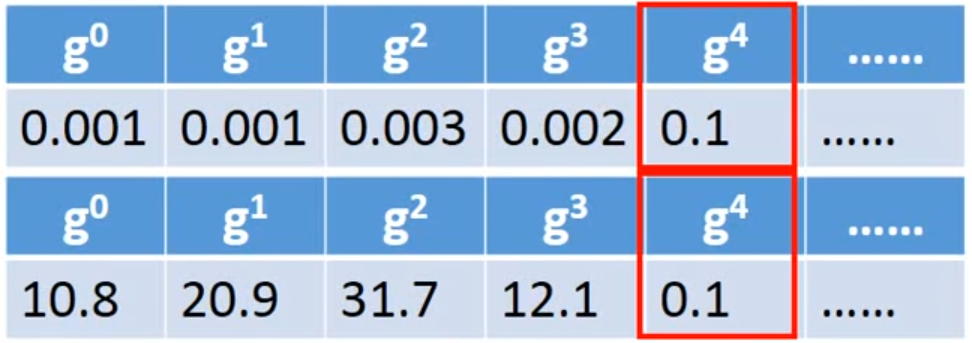

最优的步伐：

我们知道在一元二次方程中：假设一开始我们选择的点是，那么最低点的坐标就是

3、错误的来源

在制定我们的目标函数的时候，我们会遇到一些问题
比如：
我们在设置我们的模型的时候发现，我们的模型甚至连训练数据都不是大部分正确的值，说明我们这里是欠拟合（underfitting）即bias过大
我们在数据上的错误率很低，但是在测试的数据中错误率很大，说明我们是过拟合（overfitting）了。即variance大。
variance大的话，可以采用两种方法进行调整
1、增加更多的数据，训练你的模型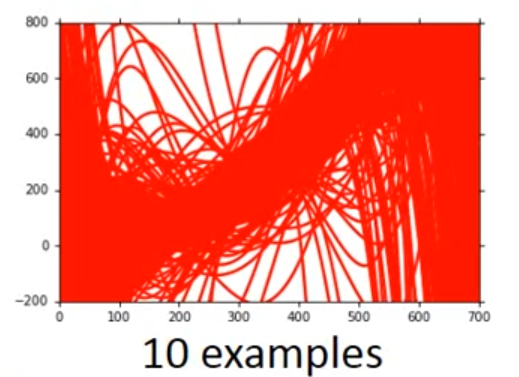


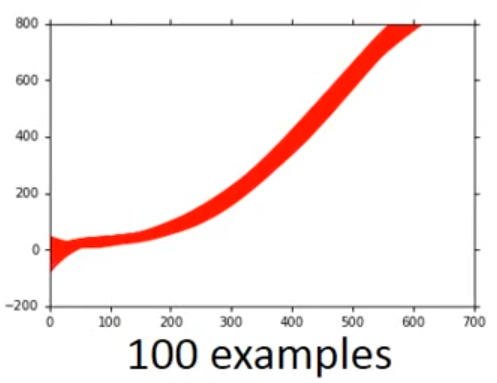
上图是数据为10与数据为100时候的模型（100个套不同的100数据，得到的100个曲线图）,我们发现增加数据，它图像更加集中了。但是数据常常不好得到，我们可以自己创造data，可以结合自己对问题的理解来增加模型的data量。
2、使用正则化
正则化有许多方法，但是现在我了解甚少。
如果bias过大，那么我们需要重新设计我们的模型
1、增加更多的特征值进入我们的模型，因为就连我们的训练数据都无法得到很好的错误率，那么我们又拿什么去预测未来的值？
2、使你的模型更加复杂。可能要考虑多次方（一次方、两次方、三次方）。

第三周

对第二周进行补充：

1、 确定步长的时候，我们无法对步长进行可视化，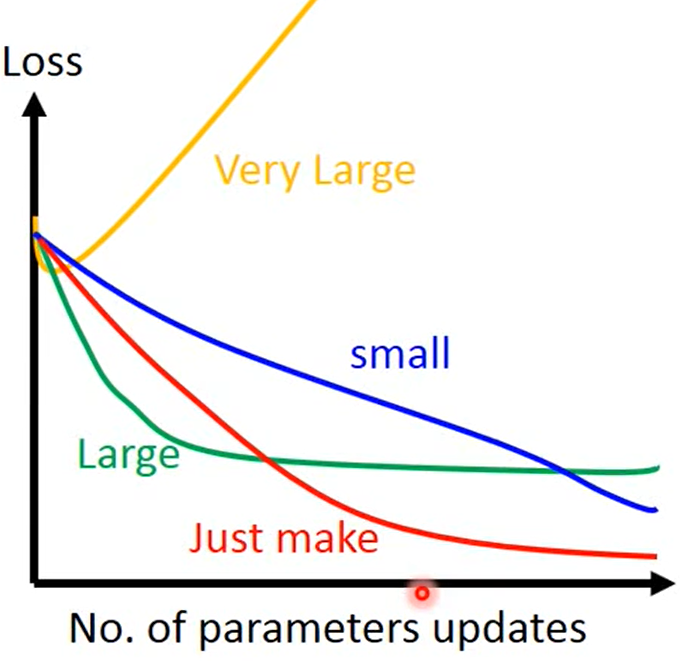

但是可以通过查看Loss函数的变化来确定，我们的步长是否找对了。
1、步长过大的话，loss就会上升
2、步长过小的话，可以达成效果，但是速度太慢。
3、刚刚好的话，就是最理想的效果
4、略大的话，可能反复横跳。

最优的步伐：

我们知道在一元二次方程中：

假设一开始我们选择的点是，那么离最低点的坐标的最佳步长就是

我们从中可以看出：实际上，上式就是：

那么与：

有什么关系吗？
显然对于：

这个并非直接充当第二次求导，而是可以反映出二次求导的变化。

梯度下降的限制：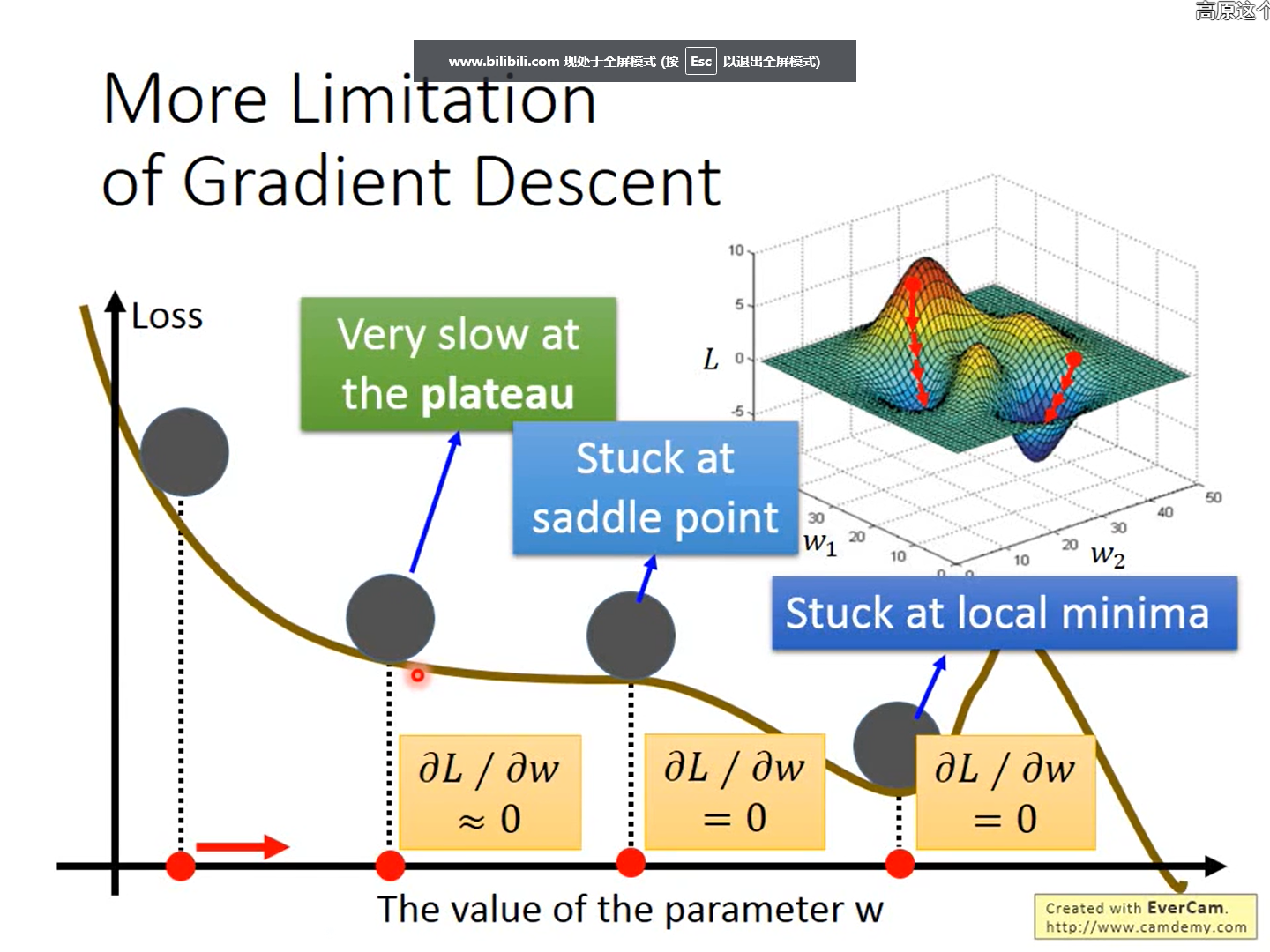

二、反向传播

并不是一个与梯度下降不同的方法，他只是一个更有效率的演算法。
首先：

然后对

进行对w求偏导：

我们取其中一个节点出来讲：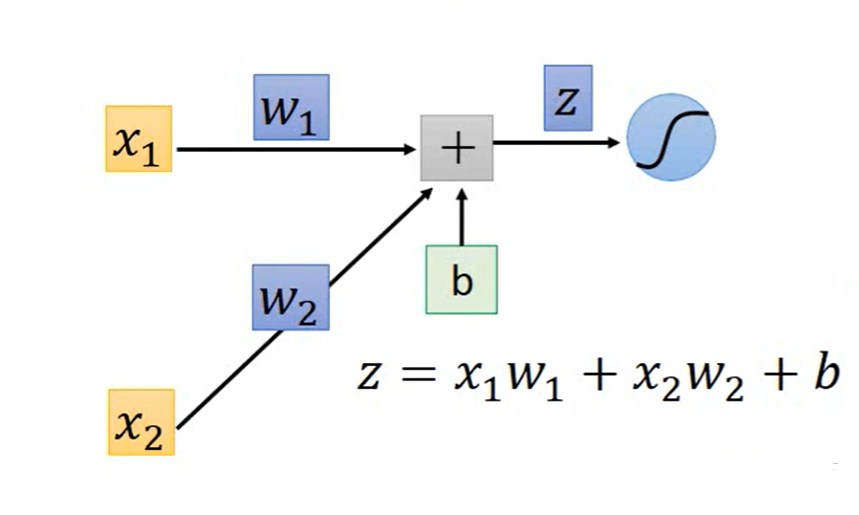


其中：我们称之为前向传播，我们称之为反向传播
然后我们进行计算，现在我们

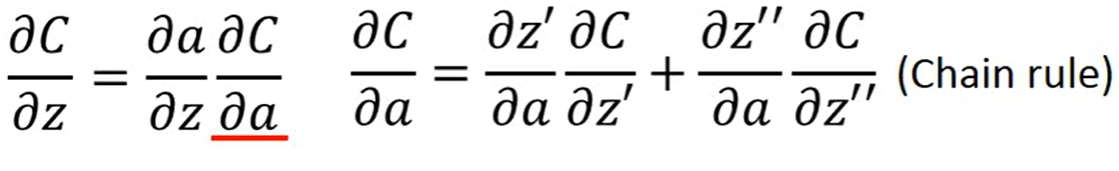
易得：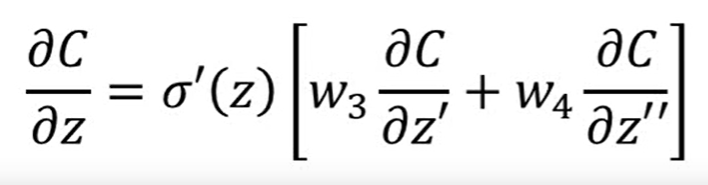

三、分类

分类问题利用回归来做的效果并不好，异常点就会影响整个回归函数。
我们要定义一个函数：

而LOSS函数为：

如果等于，L(f)=1，不等于，就为0，即让该loss函数最小时，这个模型效果就会更好。
显然我们不能进行梯度下降进行计算，因为loss函数不可微分