第三章 矩阵分解MF&因子分解机FM

3.1 矩阵分解MF

矩阵分解(Matrix Factorization，MF)技术实际上就是把用户-项目评分矩阵分解为若干个部分的组合，它在 Netfilx公司举办的推荐系统大赛上得到了广泛的应用，基于矩阵分解的推荐算法本质上是一种基于模型的协同过滤推荐算法。

基于矩阵分解的推荐算法，实现简单，预测准确度高，扩展性强，在一定程度上缓解了数据的稀疏性问题，但可解释性差。

3.1.1 隐含语义分析技术

随着用户和项目数量的急剧增长，用户和项目之间评分矩阵的维度也在在急剧增加。而由此带来的问题是计算用户与用户、项目与项目之间相似度矩阵的速度越来越慢，计算问题成为推荐系统的瓶颈。此外，随着评分矩阵越来越稀疏，推荐精度也会受到严重的影响。

对推荐系统研究过程中有很多人提出给用户或项目进行分类，但是根据传统的推荐算法很难真正发掘出用户用户潜在的兴趣度。为了解决这个问题研究人员提出从数据出发，自动找出项目的分类信息和用户的兴趣度信息。因此，隐含语义分析技术(Latent Variable Analysis） 就出现了。

隐语义模型（Latent Factor Model，LFM) 这个概念是由Netflix Prize冠军Koren在2006年提出的。隐语义模型使用一种替代的法则来发现潜在的主题或分类。隐含语义分析技术从诞生至今产生了很多著名的模型和算法。其中和该项技术相关且耳熟能详的名词有隐含主题模型(latent topic model)、矩阵分解(matrix factorization)、pLSA、LDA 等。

协同过滤算法的特点就是完全没有利用到物品本身或者是用户自身的属性，仅仅利用了用户与物品的交互信息就可以实现推荐，是一个可解释性很强，非常直观的模型，但是也存在一些问题， 第一个就是处理稀疏矩阵的能力比较弱，所以为了使得协同过滤更好处理稀疏矩阵问题， 增强泛化能力， 从协同过滤中衍生出矩阵分解模型或者叫隐语义模型, 两者差不多说的一个意思，就是在协同过滤共现矩阵的基础上， 使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。

3.1.1.1 隐语义模型

隐语义模型最早在文本领域被提出，用于找到文本的隐含语义。在2006年， 被用于推荐中， 它的核心思想是通过隐含特征（latent factor）联系用户兴趣和物品（item）， 基于用户的行为找出潜在的主题和分类， 然后对item进行自动聚类，划分到不同类别/主题(用户的兴趣)。

下面来看一个例子。如果我们知道了用户A和用户B两个用户在豆瓣的读书列表， 从他们的阅读列表可以看出，用户A的兴趣涉及侦探小说、科普图书以及一些计算机技术书， 而用户B的兴趣比较集中在数学和机器学习方面。 那么如何给A和B推荐图书呢？

先说说协同过滤算法的解法：

• 对于UserCF，首先需要找到和他们看了同样书的其他用户（兴趣相似的用户），然后给他们推荐那些用户喜欢的其他书。
• 对于ItemCF，需要给他们推荐和他们已经看的书相似的书，比如作者B看了很多关于数据挖掘的书，可以给他推荐机器学习或者模式识别方面的书。

而如果是隐语义模型的话， 它会先通过一些角度把用户兴趣和这些书归一下类， 当来了用户之后， 首先得到他的兴趣分类， 然后从这个分类中挑选他可能喜欢的书籍。

这里就看到了隐语义模型和协同过滤的不同， 这里说的角度其实就是这个隐含特征， 比如书籍的内容、作者、年份、主题等都可以算隐含特征，如果这个例子还不是很清晰的话，那么下面再举一个更为具体的例子，看看是如何通过隐含特征来划分开用户兴趣和物品的。但是在这之前，相信通过上面这个例子，我们已经隐隐约约感受到了协同过滤和隐语义模型的区别了，下面放上两种算法的原理图的对比：

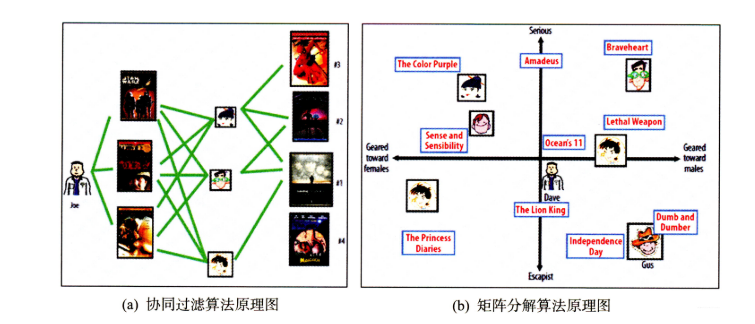
下面拿一个音乐评分的例子来具体看一下隐特征矩阵的含义。

假设每个用户都有自己的听歌偏好， 比如A喜欢带有小清新的， 吉他伴奏的， 王菲的歌曲，如果一首歌正好是王菲唱的， 并且是吉他伴奏的小清新， 那么就可以将这首歌推荐给这个用户。 也就是说是小清新， 吉他伴奏， 王菲这些元素连接起了用户和歌曲。 当然每个用户对不同的元素偏好不同， 每首歌包含的元素也不一样， 所以我们就希望找到下面的两个矩阵：

1. 潜在因子—— 用户矩阵Q
   这个矩阵表示不同用户对于不同元素的偏好程度， 1代表很喜欢， 0代表不喜欢， 比如下面这样：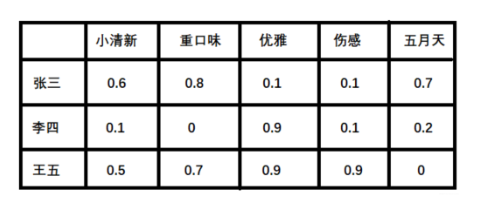
   
2. 潜在因子——音乐矩阵P
   表示每种音乐含有各种元素的成分，比如下表中，音乐A是一个偏小清新的音乐， 含有小清新的Latent Factor的成分是0.9，重口味的成分是0.1，优雅成分0.2…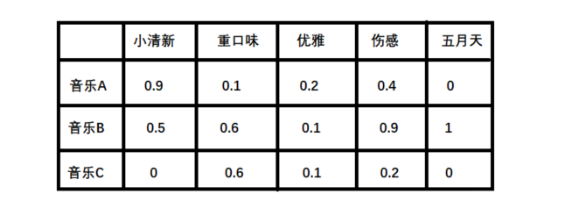
   

利用上面的两个矩阵，我们就能得到张三对音乐A的喜爱程度：

张三对小清新的偏好 * 音乐A含有小清新的成分 + 张三对重口味的偏好 * 音乐A含有重口味的成分 + 张三对优雅的偏好 * 音乐A含有优雅的成分…,

下面是对应的两个隐向量：

根据隐向量其实就可以得到张三对音乐A的打分，即：

0.6∗0.9+0.8∗0.1+0.1∗0.2+0.1∗0.4+0.7∗0=0.69

按照这个计算方式， 每个用户对每首歌其实都可以得到这样的分数，最后就得到了我们的评分矩阵：

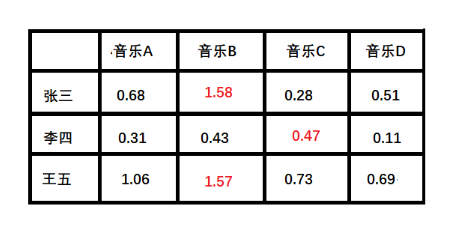
这里的红色表示用户没有打分，我们通过隐向量计算得到的。

上面例子中的小清晰、 重口味、 优雅这些就可以看做是隐含特征， 而通过这个隐含特征就可以把用户的兴趣和音乐的进行一个分类，其实就是找到了每个用户每个音乐的一个隐向量表达形式（embedding的原理其实也是这样，那里是找到每个词的隐向量表达），这个隐向量就可以反映出用户的兴趣和物品的风格，并能将相似的物品推荐给相似的用户等。所以，矩阵分解算法MF就是把协同过滤算法进行了一种延伸，把用户的相似性和物品的相似性通过了一个叫做隐向量的方式进行表达。

但是，真实的情况下我们其实是没有上面那两个矩阵的，音乐那么多，用户那么多， 我们没有办法去找一些隐特征去表示出这些东西，另外一个问题就是即使能表示也不一定准，对于每个用户或者每个物品的风格，我们每个人都有不同的看法。所以事实上，我们有的只有用户的评分矩阵，也就是最后的结果，并且一般这种矩阵长这样：

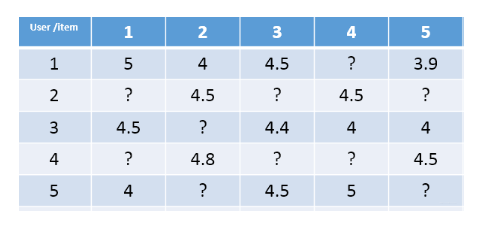
这种矩阵非常的稀疏，如果直接基于用户相似性或者物品相似性去填充这个矩阵是不太容易的， 并且很容易出现长尾问题， 所以矩阵分解就可以比较容易的解决这个问题。

矩阵分解模型其实就是在想办法基于这个评分矩阵去找到上面例子中的那两个矩阵， 也就是用户兴趣和物品的隐向量表达， 然后就把这个评分矩阵分解成Q和P两个矩阵乘积的形式， 这时候就可以基于这两个矩阵去预测某个用户对某个物品的评分了。 然后基于这个评分去进行推荐。这就是矩阵分解算法的原理。

3.1.1.2 矩阵分解算法

在矩阵分解的算法框架下， 我们就可以通过分解协同过滤的共现矩阵来得到用户和物品的隐向量， 就是上面的用户矩阵Q和物品矩阵P，这也是“矩阵分解”名字的由来。

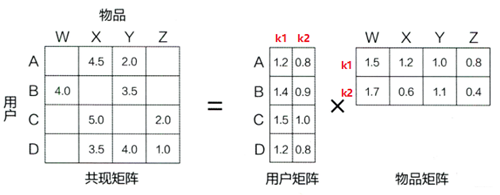
矩阵分解算法将 m×n 维的共现矩阵 R 分解成 m×k 维的用户矩阵 U 和 k×n 维的物品矩阵 V 相乘的形式。其中 m 是用户数量，n 是物品数量，k 是隐向量维度，也就是隐含特征个数，只不过这里的隐含特征变得不可解释了，即我们不知道具体含义了，要模型自己去学。k 的大小决定了隐向量表达能力的强弱，k 越大，表达信息就越强，理解起来就是把用户的兴趣和物品的分类划分的越具体。

那么如果有了用户矩阵和物品矩阵的话，我们就知道了如果想计算用户 u 对物品 i 的评分， 只需要计算

%3Dr%7Bu%20i%7D%3Dp%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%3D%5Csum%7Bf%3D1%7D%5E%7BF%7D%20p%7Bu%2C%20k%7D%20q%7Bk%2Ci%7D%0A#card=math&code=%5Coperatorname%7BPreference%7D%28u%2C%20i%29%3Dr%7Bu%20i%7D%3Dp%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%3D%5Csum%7Bf%3D1%7D%5E%7BF%7D%20p%7Bu%2C%20k%7D%20q%7Bk%2Ci%7D%0A&id=w2O0E)

这里的 就是用户 u 的隐向量， 就类似于上面的张三向量，注意这是列向量， 是物品 i 的隐向量，就类似于上面的音乐A向量， 这个也是列向量，所以才用了 得到了一个数，也就是用户的最终评分， 计算过程其实和上面例子中一样。这里的 和 是模型的参数， 也正是我们想办法要计算的， 度量的是用户 u 的兴趣和第 k 个隐类的关系，而 度量了第 k 个隐类和物品 i 之间的关系。

3.1.1.3 矩阵分解算法

谈到矩阵分解，最常用的方法是特征值分解(EVD)或者奇异值分解(SVD），但是这两种方式在这里不适用。

首先是EVD，它要求分解的矩阵是方阵，显然用户-物品矩阵不满足这个要求，而传统的SVD分解，会要求原始矩阵是稠密的，而我们这里的这种矩阵一般情况下是非常稀疏的，如果想用奇异值分解，就必须对缺失的元素进行填充，而一旦补全，空间复杂度就会非常高，且补的不一定对。然后就是SVD分解计算复杂度非常高，而我们的用户-物品矩阵非常大，所以基本上无法使用。

3.1.2 Funk-SVD算法

2006年的Netflix Prize之后， Simon Funk公布了一个矩阵分解算法叫做Funk-SVD, 后来被Netflix Prize的冠军Koren称为Latent Factor Model ( LFM )。 Funk-SVD的思想很简单： 把求解上面两个矩阵的参数问题转换成一个最优化问题， 可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵。

在前一节我们知道，如果有了用户矩阵和物品矩阵的话，我们就知道了如果想计算用户u对物品i的评分，只需要

%3Dr%7Bu%20i%7D%3Dp%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%3D%5Csum%7Bf%3D1%7D%5E%7BF%7D%20p%7Bu%2C%20k%7D%20q%7Bk%2Ci%7D%0A#card=math&code=%5Coperatorname%7BPreference%7D%28u%2C%20i%29%3Dr%7Bu%20i%7D%3Dp%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%3D%5Csum%7Bf%3D1%7D%5E%7BF%7D%20p%7Bu%2C%20k%7D%20q%7Bk%2Ci%7D%0A&id=mDwlX)

而现在，我们有真实的, 但是没有, 那么我们可以随机初始化一个用户矩阵 U 和一个物品矩阵 V ，然后不就有了？当然，随机初始化的肯定不准啊，但是，有了之后，我们就可以计算一个猜测的 , 即

这个值肯定是不准的，那么这个猜测的和真实值之间就会有一个误差：

有了误差，我们就可以计算出总的误差平方和：

%5E%7B2%7D%0A#card=math&code=%5Coperatorname%7BSSE%7D%3D%5Csum%7Bu%2C%20i%7D%20e%7Bu%20i%7D%5E%7B2%7D%3D%5Csum%7Bu%2C%20i%7D%5Cleft%28r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q_%7Bk%2C%20i%7D%5Cright%29%5E%7B2%7D%0A&id=Ofksa)

有了损失，我们就可以想办法进行训练，把SSE降到最小，那么我们的两个矩阵参数就可以算出来。所以就把这个问题转成了最优化的的问题，而我们的目标函数就是：

%20%5Cin%20K%7D%5Cleft(%5Cboldsymbol%7Br%7D%7B%5Cmathrm%7Bui%7D%7D-p%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%5Cright)%5E%7B2%7D%0A#card=math&code=%5Cmin%20%7B%5Cboldsymbol%7Bq%7D%5E%7B%2A%7D%2C%20%5Cboldsymbol%7Bp%7D%5E%7B%2A%7D%7D%20%5Csum%7B%28u%2C%20i%29%20%5Cin%20K%7D%5Cleft%28%5Cboldsymbol%7Br%7D%7B%5Cmathrm%7Bui%7D%7D-p%7Bu%7D%5E%7BT%7D%20q%7Bi%7D%5Cright%29%5E%7B2%7D%0A&id=SPDlu)

这里的表示所有用户评分样本的集合。

有了目标函数，那么我们就可以使用梯度下降算法来降低损失。那么我们需要对目标函数求偏导，得到梯度。我们的目标函数如果是上面的SSE，我们下面来推导一下最后的导数：

%5E%7B2%7D%0A#card=math&code=%5Coperatorname%7BSSE%7D%3D%5Csum%7Bu%2C%20i%7D%20e%7Bu%20i%7D%5E%7B2%7D%3D%5Csum%7Bu%2C%20i%7D%5Cleft%28r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q_%7Bk%2Ci%7D%5Cright%29%5E%7B2%7D%0A&id=DORwl)

首先我们求SSE在（也就是Q矩阵的第 u 行 k 列）的梯度：

%20%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%20e%7Bu%20i%7D%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%5Cleft(r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q%7Bk%2Ci%7D%5Cright)%3D-2e%7Bu%20i%7D%20q%7Bk%2Ci%7D%0A#card=math&code=%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%20S%20S%20E%3D%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%5Cleft%28e%7Bu%20i%7D%5E%7B2%7D%5Cright%29%20%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%20e%7Bu%20i%7D%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bu%2Ck%7D%7D%5Cleft%28r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q%7Bk%2Ci%7D%5Cright%29%3D-2e%7Bu%20i%7D%20q_%7Bk%2Ci%7D%0A&id=VXoq7)

然后求SSE在处（也就是V矩阵的第 k 行 i 列）的梯度：

%20%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bk%2Ci%7D%7D%20e%7Bu%20i%7D%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bk%2Ci%7D%7D%5Cleft(r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q%7Bk%2Ci%7D%5Cright)%3D-2e%7Bu%20i%7D%20p%7Bu%2Ck%7D%0A#card=math&code=%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20q%7Bk%2Ci%7D%7D%20S%20S%20E%3D%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bk%2Ci%7D%7D%5Cleft%28e%7Bu%20i%7D%5E%7B2%7D%5Cright%29%20%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bk%2Ci%7D%7D%20e%7Bu%20i%7D%3D2e%7Bu%20i%7D%20%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20p%7Bk%2Ci%7D%7D%5Cleft%28r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%2Ck%7D%20q%7Bk%2Ci%7D%5Cright%29%3D-2e%7Bu%20i%7D%20p_%7Bu%2Ck%7D%0A&id=GtqTM)

为了让公式更为简单， 把前面的2约掉， 即可以令SSE等于：

%5E%7B2%7D%0A#card=math&code=%5Coperatorname%7BSSE%7D%3D%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bu%2C%20i%7D%20e%7Bu%20i%7D%5E%7B2%7D%3D%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bu%2C%20i%7D%5Cleft%28r%7Bu%20i%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20p%7Bu%20k%7D%20q_%7Bk%20i%7D%5Cright%29%5E%7B2%7D%0A&id=qba24)

这时候， 梯度就没有前面的系数了，有了梯度，接下来我们就可以用梯度下降算法更新梯度了：

%3Dp%7Bu%2Ck%7D%2B%5Ceta%20e%7Bui%7Dq%7Bk%2Ci%7D%20%5C%5C%20q%7Bk%2C%20i%7D%3Dq%7Bk%2C%20i%7D-%5Ceta%20(-e%7Bui%7Dp%7Bu%2Ck%7D)%3Dq%7Bk%2C%20i%7D%2B%5Ceta%20e%7Bui%7Dp%7Bu%2Ck%7D%0A#card=math&code=p%7Bu%2C%20k%7D%3Dp%7Bu%2Ck%7D-%5Ceta%20%28-e%7Bui%7Dq%7Bk%2Ci%7D%29%3Dp%7Bu%2Ck%7D%2B%5Ceta%20e%7Bui%7Dq%7Bk%2Ci%7D%20%5C%5C%20q%7Bk%2C%20i%7D%3Dq%7Bk%2C%20i%7D-%5Ceta%20%28-e%7Bui%7Dp%7Bu%2Ck%7D%29%3Dq%7Bk%2C%20i%7D%2B%5Ceta%20e%7Bui%7Dp%7Bu%2Ck%7D%0A&id=Vvcep)

这里的 η 是学习率，控制步长用的，但上面这个有个问题就是当参数很多的时候， 就是两个矩阵很大的时候，往往容易陷入过拟合的困境，这时候，就需要在目标函数上面加上正则化的损失，就变成了RSVD，关于RSVD的详细内容，由于篇幅原因，这里不再过多的赘述。

3.1.3 Bias SVD算法

在实际中，单纯的是不够的，还要考虑其他的一些因素，比如一个评分系统，有些固有的属性和用户物品无关，而用户也有些属性和物品无关，物品也有些属性和用户无关。因此， Netfix Prize中提出了另一种LFM，在原来的基础上加了偏置项， 来消除用户和物品打分的偏差，即预测公式如下：

这个预测公式加入了3项偏置 , 作用如下：

• μ : 训练集中所有记录的评分的全局平均数。在不同网站中，因为网站定位和销售物品不同，网站的整体评分分布也会显示差异。比如有的网站中用户就喜欢打高分，有的网站中用户就喜欢打低分。而全局平均数可以表示网站本身对用户评分的影响。
• : 用户偏差系数，可以使用用户 u 给出的所有评分的均值，也可以当做训练参数。这一项表示了用户的评分习惯中和物品没有关系的那种因素。比如有些用户比较苛刻，对什么东西要求很高，那么他评分就会偏低，而有些用户比较宽容，对什么东西都觉得不错，那么评分就偏高
• : 物品偏差系数， 可以使用物品 i 收到的所有评分的均值， 也可以当做训练参数。 这一项表示了物品接受的评分中和用户没有关系的因素。 比如有些物品本身质量就很高， 因此获得的评分相对比较高， 有的物品本身质量很差， 因此获得的评分相对较低。

加了用户和物品的打分偏差之后， 矩阵分解得到的隐向量更能反映不同用户对不同物品的“真实”态度差异， 也就更容易捕捉评价数据中有价值的信息， 从而避免推荐结果有偏。 注意此时的SSE会发生变化:

%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%5Cleft%7C%5Cboldsymbol%7Bp%7D%7Bu%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bi%7D%5Cleft%7C%5Cboldsymbol%7Bq%7D%7Bi%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B%5Cmathbf%7B1%7D%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D%7Bu%7D%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D%7Bi%7D%5E%7B2%7D%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7D%0A%5Coperatorname%7BSSE%7D%3D%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bu%2C%20i%7D%20e%7Bu%20i%7D%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%5Cleft%7C%5Cboldsymbol%7Bp%7D%7Bu%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bi%7D%5Cleft%7C%5Cboldsymbol%7Bq%7D%7Bi%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D%7Bu%7D%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D%7Bi%7D%5E%7B2%7D%20%5C%5C%0A%3D%5Cfrac%7B1%7D%7B2%7D%20%5Csum%7Bu%2C%20i%7D%5Cleft%28%5Cboldsymbol%7Br%7D%7Bu%20i%7D-%5Cboldsymbol%7B%5Cmu%7D-%5Cboldsymbol%7Bb%7D%7Bu%7D-%5Cboldsymbol%7Bb%7D%7Bi%7D-%5Csum%7Bk%3D1%7D%5E%7BK%7D%20%5Cboldsymbol%7Bp%7D%7Bu%20k%7D%20%5Cboldsymbol%7Bq%7D%7Bk%20i%7D%5Cright%29%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%5Cleft%7C%5Cboldsymbol%7Bp%7D%7Bu%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bi%7D%5Cleft%7C%5Cboldsymbol%7Bq%7D%7Bi%7D%5Cright%7C%5E%7B2%7D%2B%5Cfrac%7B%5Cmathbf%7B1%7D%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D%7Bu%7D%5E%7B2%7D%2B%5Cfrac%7B1%7D%7B2%7D%20%5Clambda%20%5Csum%7Bu%7D%20%5Cboldsymbol%7Bb%7D_%7Bi%7D%5E%7B2%7D%0A%5Cend%7Barray%7D%0A&id=dsLud)

此时如果把和当做训练参数的话， 那么它们的梯度是：

更新公式为：

%20%5C%5C%0A%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%20%26%3D%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%2B%5Cboldsymbol%7B%5Ceta%7D%5Cleft(%5Cboldsymbol%7Be%7D%7B%5Cboldsymbol%7Bu%7D%20i%7D-%5Clambda%20%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%5Cright)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cboldsymbol%7Bb%7D%7Bu%7D%26%3D%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bu%7D%7D%2B%5Cboldsymbol%7B%5Ceta%7D%5Cleft%28%5Cboldsymbol%7Be%7D%7Bu%20i%7D-%5Clambda%20%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bu%7D%7D%5Cright%29%20%5C%5C%0A%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%20%26%3D%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%2B%5Cboldsymbol%7B%5Ceta%7D%5Cleft%28%5Cboldsymbol%7Be%7D%7B%5Cboldsymbol%7Bu%7D%20i%7D-%5Clambda%20%5Cboldsymbol%7Bb%7D%7B%5Cboldsymbol%7Bi%7D%7D%5Cright%29%0A%5Cend%7Baligned%7D%0A&id=pxCDG)

其中，是和的学习率。

而对于和，导数没有变化，更新公式也没有变化。

3.1.4 编程实现

现在用代码实现一下上面的算法来预测上一章里预测Alice对物品5的评分， 看看矩阵分解到底是怎么进行预测或者是推荐的。

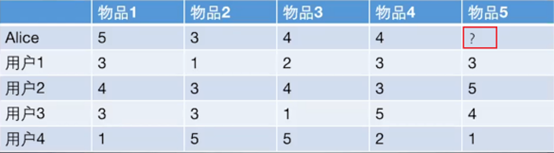
任务就是根据这个评分矩阵， 猜测Alice对物品5的打分。

在实现SVD之前， 先来回忆一下ItemCF和UserCF对于这个问题的做法， 首先ItemCF的做法，根据已有的用户打分计算物品之间的相似度，得到物品的相似度矩阵， 根据这个相似度矩阵，选择出前K个与物品5最相似的物品，然后基于Alice对这K个物品的得分，猜测Alice对物品5的得分，有一个加权的计算公式；UserCF的做法是根据用户对其他物品的打分，计算用户之间的相似度，选择出与Alice最相近的K个用户， 然后基于那K个用户对物品5的打分计算出Alice对物品5的打分。但是，这两种方式有个问题， 就是如果矩阵非常稀疏的话，当然这个例子是个特例，一般矩阵都是非常稀疏的， 那么预测效果就不好，因为两个相似用户对同一物品打分的概率以及Alice同时对两个相似物品打分的概率可能都比较小。另外，这两种方法显然没有考虑到全局的物品或者用户，只是基于了最相似的例子，很可能有偏。

那么SVD在解决这个问题上是这么做的：

1. 首先，它会先初始化用户矩阵P和物品矩阵Q， P的维度是[users_num, F], Q的维度是[item_nums, F]，这个F是隐向量的维度。 也就是把通过隐向量的方式把用户的兴趣和F的特点关联了起来。初始化这两个矩阵的方式很多， 但根据经验， 随机数需要和1/sqrt(F)成正比，下面代码中会发现。
2. 有了两个矩阵之后，我就可以根据用户已经打分的数据去更新参数，这就是训练模型的过程。方法很简单，就是遍历用户，对于每个用户，遍历它打分的物品，这样就拿到了该用户和物品的隐向量， 然后两者相乘加上偏置就是预测的评分， 这时候与真实评分有个差距， 根据上面的梯度下降就可以进行参数的更新。

这样训练完之后，我们就可以得到用户Alice和物品5的隐向量，根据这个就可以预测Alice对物品5的打分。下面的代码的逻辑就是上面这两步，这里使用带有偏置项和正则项的那个SVD算法：

import math
import random
class SVD():
    def __init__(self, rating_data, F=5, alpha=0.1, lmbda=0.1, max_iter=100):
        self.F = F           # 这个表示隐向量的维度
        self.P = dict()          #  用户矩阵P  大小是[users_num, F]
        self.Q = dict()     # 物品矩阵Q  大小是[item_nums, F]
        self.bu = dict()   # 用户偏差系数
        self.bi = dict()    # 物品偏差系数
        self.mu = 1.0        # 全局偏差系数
        self.alpha = alpha   # 学习率
        self.lmbda = lmbda    # 正则项系数
        self.max_iter = max_iter    # 最大迭代次数
        self.rating_data = rating_data # 评分矩阵
        # 初始化矩阵P和Q, 方法很多， 一般用随机数填充， 但随机数大小有讲究， 根据经验， 随机数需要和1/sqrt(F)成正比
        cnt = 0    # 统计总的打分数， 初始化mu用
        for user, items in self.rating_data.items():
            self.P[user] = [random.random() / math.sqrt(self.F)  for x in range(0, F)]
            self.bu[user] = 0
            cnt += len(items) 
            for item, rating in items.items():
                if item not in self.Q:
                    self.Q[item] = [random.random() / math.sqrt(self.F) for x in range(0, F)]
                    self.bi[item] = 0
        self.mu /= cnt
    # 有了矩阵之后， 就可以进行训练, 这里使用随机梯度下降的方式训练参数P和Q
    def train(self):
        for step in range(self.max_iter):
            for user, items in self.rating_data.items():
                for item, rui in items.items():
                    rhat_ui = self.predict(user, item)   # 得到预测评分
                    # 计算误差
                    e_ui = rui - rhat_ui
                    self.bu[user] += self.alpha * (e_ui - self.lmbda * self.bu[user])
                    self.bi[item] += self.alpha * (e_ui - self.lmbda * self.bi[item])
                    # 随机梯度下降更新梯度
                    for k in range(0, self.F):
                        self.P[user][k] += self.alpha * (e_ui*self.Q[item][k] - self.lmbda * self.P[user][k])
                        self.Q[item][k] += self.alpha * (e_ui*self.P[user][k] - self.lmbda * self.Q[item][k])
            self.alpha *= 0.1    # 每次迭代步长要逐步缩小
    # 预测user对item的评分， 这里没有使用向量的形式
    def predict(self, user, item):
        return sum(self.P[user][f] * self.Q[item][f] for f in range(0, self.F)) + self.bu[user] + self.bi[item] + self.mu

下面建立一个字典来存放数据，之所以用字典， 是因为很多时候矩阵非常的稀疏， 如果用pandas的话， 会出现很多Nan的值， 反而不好处理。

# 定义数据集， 也就是那个表格， 注意这里我们采用字典存放数据， 因为实际情况中数据是非常稀疏的， 很少有情况是现在这样
def loadData():
    rating_data={1: {'A': 5, 'B': 3, 'C': 4, 'D': 4},
           2: {'A': 3, 'B': 1, 'C': 2, 'D': 3, 'E': 3},
           3: {'A': 4, 'B': 3, 'C': 4, 'D': 3, 'E': 5},
           4: {'A': 3, 'B': 3, 'C': 1, 'D': 5, 'E': 4},
           5: {'A': 1, 'B': 5, 'C': 5, 'D': 2, 'E': 1}
          }
    return rating_data
# 接下来就是训练和预测
rating_data = loadData()
basicsvd = SVD(rating_data, F=10)
basicsvd.train()
for item in ['E']:
    print(item, basicsvd.predict(1, item))
# 结果：
E 3.0985554725354505

通过这个方式，得到的预测评分是3.10，这个和隐向量的维度，训练次数和训练方式有关。

3.2 因子分解机FM

因子分解机（Factorization Machines） 是由 Steffen Rendle于2010年提出一种因子分解模型，其目的是解决传统的因子分解模型的一些缺点。首先，传统的因子模型,每遇到一种新问题,都需要在矩阵分解的基础上建立一个新模型(例如上一节的SVD)，推导出新的参数学习算法，并在学习参数过程中调节各种参数。以至于这些因子分解模型对于那些对因子分解模型的使用不是很熟悉的人来说是费事、耗力、易错的；其次，传统的因子分解模型不能很好地利用特征工程法（ feature engineering）来完成学习任务。在实际的机器学习任务中，常用的方法是首先用特征向量来表示数据，然后用一些开源工具 LibSVM或Weka等工具进行学习，方便地完成分类或决策任务。

FM的优势在于它能够通过特征向量去模拟因子分解模型，它既结合了特征工程法的普遍性和适用性，又能够利用因子分解模型对不同类别的变量之间的交互作用（interaction)进行建模估计，借助开源实现工具 libFM，能够快速地完成学习任务，取得很好的精度。将这一模型命名为因子分解机，作者正是希望该模型能像支持向量机那样简单、易用、高精度。

3.2.1 FM模型的引入

3.2.1.1 逻辑回归模型及其缺点

FM模型其实是一种思路，具体的应用稍少。一般来说做推荐CTR预估时最简单的思路就是将特征做线性组合（逻辑回归LR），传入sigmoid中得到一个概率值，本质上这就是一个线性模型，因为sigmoid是单调增函数不会改变里面的线性模型的CTR预测顺序，因此逻辑回归模型效果会比较差。也就是LR的缺点有：

• 是一个线性模型
• 每个特征对最终输出结果独立，需要手动特征交叉（），比较麻烦

3.2.1.2 二阶交叉项的考虑及改进

LR模型的上述缺陷（主要是手动做特征交叉比较麻烦），干脆就考虑所有的二阶交叉项，也就是将目标函数由原来的

变为

但这个式子有一个问题，只有当与均不为0时这个二阶交叉项才会生效，后面这个特征交叉项本质是和多项式核SVM等价的，为了解决这个问题，我们的FM登场了！

FM模型使用了如下的优化函数：

上式做的改动就是把 替换成了 ，大家应该就看出来了，这实际上就有深度学习的意味在里面了，实质上就是给每个 计算一个embedding，然后将两个向量之间的embedding做内积得到之前所谓的 ，好处就是这个模型泛化能力强 ，即使两个特征之前从未在训练集中同时出现，我们也不至于像之前一样训练不出 ，事实上只需要 和其他的 同时出现过就可以计算出 的embedding。

3.2.2 FM公式的理解

从公式来看，模型前半部分就是普通的LR线性组合，后半部分的交叉项特征组合。首先，单从模型表达能力上来看，FM是要强于LR的，至少它不会比LR弱，当交叉项参数全为0的时候，整个模型就退化为普通的LR模型。对于有n个特征的模型，特征组合的参数数量共有%7D%7B2%7D#card=math&code=1%2B2%2B3%2B%5Ccdots%20%20%2B%20n-1%3D%5Cfrac%7Bn%28n-1%29%7D%7B2%7D&id=nKztd)个，并且任意两个参数之间是独立的。所以说特征数量比较多的时候，特征组合之后，维度自然而然就高了。

这里补充一个定理：

• 任意一个实对称矩阵（正定矩阵）都存在一个矩阵，使得 成立。

类似地，所有二次项参数 可以组成一个对称阵（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为 $W=V^TV $， 的第列( )便是第维特征( )的隐向量。

%20%3D%20%5Comega%7B0%7D%2B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%5Comega%7Bi%7Dx%7Bi%7D%7D%2B%5Csum%7Bi%3D1%7D%5E%7Bn-1%7D%7B%5Csum%7Bj%3Di%2B1%7D%5E%7Bn%7D%20%5Ccolor%7Bred%7D%7B%3Cv%7Bi%7D%2Cv%7Bj%7D%3Ex%7Bi%7Dx%7Bj%7D%7D%7D%0A#card=math&code=%5Chat%7By%7D%28X%29%20%3D%20%5Comega%7B0%7D%2B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%5Comega%7Bi%7Dx%7Bi%7D%7D%2B%5Csum%7Bi%3D1%7D%5E%7Bn-1%7D%7B%5Csum%7Bj%3Di%2B1%7D%5E%7Bn%7D%20%5Ccolor%7Bred%7D%7B%3Cv%7Bi%7D%2Cv%7Bj%7D%3Ex%7Bi%7Dx%7Bj%7D%7D%7D%0A&id=uYbfq)

，，，是长度为的两个向量的点乘，公式如下：

其中，

• 为全局偏置；
• 是模型第个变量的权重;
• 特征和的交叉权重;
• $v_{i} i$维特征的隐向量;
• 代表向量点积;
• #card=math&code=k%28k%3C%3Cn%29&id=I3I9Q)为隐向量的长度，包含 个描述特征的因子。

FM模型中二次项的参数数量减少为 $kn $个，远少于多项式模型的参数数量。另外，参数因子化使得 的参数和 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说， 和 的系数分别为 和 ，它们之间有共同项 。也就是说，所有包含“ 的非零组合特征”（存在某个 ，使得 ）的样本都可以用来学习隐向量，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中, 和 是相互独立的。

显而易见，FM的公式是一个通用的拟合方程，可以采用不同的损失函数用于解决regression、classification等问题，比如可以采用MSE（Mean Square Error）loss function来求解回归问题，也可以采用Hinge/Cross-Entropy loss来求解分类问题。当然，在进行二元分类时，FM的输出需要使用sigmoid函数进行变换，该原理与LR是一样的。直观上看，FM的复杂度是 #card=math&code=O%28kn%5E2%29&id=mdCem) 。但是FM的二次项可以化简，其复杂度可以优化到 #card=math&code=O%28kn%29&id=eC5cR) 。由此可见，FM可以在线性时间对新样本作出预测。

证明：

%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7B%5Cleft%5B%20%5Cleft(%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7Dx_i%7D%20%5Cright)%20%5Ccdot%20%5Cleft(%20%5Csum%7Bj%3D1%7D%5E%7Bn%7D%7Bv%7Bj%2Cf%7Dx_j%7D%20%5Cright)%20-%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7D%5E2%20x_i%5E2%7D%20%5Cright%5D%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7B%5Cleft%5B%20%5Cleft(%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7Dxi%7D%20%5Cright)%5E2%20-%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7D%5E2%20x_i%5E2%7D%20%5Cright%5D%7D%20%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%20%5Csum%7Bi%3D1%7D%5E%7Bn-1%7D%7B%5Csum%7Bj%3Di%2B1%7D%5E%7Bn%7D%7B%3Cv_i%2Cv_j%3Ex_ix_j%7D%7D%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%5Csum%7Bj%3D1%7D%5E%7Bn%7D%7B%3Cv_i%2Cv_j%3Ex_ix_j%7D%7D%20-%20%5Cfrac%7B1%7D%7B2%7D%20%7B%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%3Cvi%2Cv_i%3Ex_ix_i%7D%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%20%5Cleft%28%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%5Csum%7Bj%3D1%7D%5E%7Bn%7D%7B%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7Bv%7Bi%2Cf%7Dv%7Bj%2Cf%7Dxix_j%7D%7D%7D%20-%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7B%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7Bv%7Bi%2Cf%7Dv%7Bi%2Cf%7Dx_ix_i%7D%7D%20%5Cright%29%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7B%5Cleft%5B%20%5Cleft%28%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7Dxi%7D%20%5Cright%29%20%5Ccdot%20%5Cleft%28%20%5Csum%7Bj%3D1%7D%5E%7Bn%7D%7Bv%7Bj%2Cf%7Dx_j%7D%20%5Cright%29%20-%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7D%5E2%20x_i%5E2%7D%20%5Cright%5D%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7B1%7D%7B2%7D%5Csum%7Bf%3D1%7D%5E%7Bk%7D%7B%5Cleft%5B%20%5Cleft%28%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv%7Bi%2Cf%7Dxi%7D%20%5Cright%29%5E2%20-%20%5Csum%7Bi%3D1%7D%5E%7Bn%7D%7Bv_%7Bi%2Cf%7D%5E2%20x_i%5E2%7D%20%5Cright%5D%7D%20%5Cend%7Balign%7D%0A&id=Mvmdl)

上述证明的说明如下，

• 是一个具体的值；
• 第1个等号：对称矩阵 对角线上半部分；
• 第2个等号：把向量内积 , 展开成累加和的形式；
• 第3个等号：提出公共部分；
• 第4个等号： 和 相当于是一样的，表示成平方过程。

3.2.3 FM模型的应用

最直接的想法就是直接把FM得到的结果放进sigmoid中输出一个概率值，由此做CTR预估，事实上我们也可以做召回。

由于FM模型是利用两个特征的Embedding做内积得到二阶特征交叉的权重，那么我们可以将训练好的FM特征取出离线存好，之后用来做KNN向量检索。

工业应用的具体操作步骤：

• 离线训练好FM模型（学习目标可以是CTR）
• 将训练好的FM模型Embedding取出
• 将每个uid对应的Embedding做avg pooling（平均）形成该用户最终的Embedding，item也做同样的操作
• 将所有的Embedding向量放入Faiss等
• 线上uid发出请求，取出对应的user embedding，进行检索召回

3.2.4 使用pyFM库实现FM

• 安装：
  这里采用手动安装的方式，具体操作如下
  • 在https://github.com/coreylynch/pyFM中手动下载包
  • 将包解压，更改里面的setup.py文件，去掉setup.py文件里面的libraries=[“m”]一行
  • cd到当前文件夹下`python setup.py install

• 测试
  这部分主要介绍下如何使用这个包
  第一步：导包

  from pyfm import pylibfm
  from sklearn.feature_extraction import DictVectorizer
  import numpy as np

• 第二步：创建训练集并转换成one-hot编码的特征形式 ```python train = [ {“user”: “1”, “item”: “5”, “age”: 19}, {“user”: “2”, “item”: “43”, “age”: 33}, {“user”: “3”, “item”: “20”, “age”: 55}, {“user”: “4”, “item”: “10”, “age”: 20}, ] v = DictVectorizer() X = v.fit_transform(train) print(X.toarray())

‘’’ [[19. 0. 0. 0. 1. 1. 0. 0. 0.] [33. 0. 0. 1. 0. 0. 1. 0. 0.] [55. 0. 1. 0. 0. 0. 0. 1. 0.] [20. 1. 0. 0. 0. 0. 0. 0. 1.]] ‘’’

- **第三步：创建标签**<br />这里简单创建了一个全1的标签： 
```python
y = np.repeat(1.0, X.shape[0])
y

• 第四步：训练并预测
  就和调用sklearn的包是一样的用法：

  fm = pylibfm.FM()
  fm.fit(X, y)
  fm.predict(v.transform({"user": "1", "item": "10", "age": 24}))
  # array([0.99101363])
  

3.2.4.1 电影评分数据集实战

这里同样采用movielens数据集进行代码实战，主要步骤的代码如下：

• 导包，并定义一个导入指定格式数据集的函数
  ```python import numpy as np from sklearn.feature_extraction import DictVectorizer from pyfm import pylibfm

读取数据

def dataLoader(filename, path=’./dataset/ml-100k/‘): data = [] y = [] users = set() items = set() with open(path+filename) as f: for line in f: (user, movie_id, rating, ts) = line.split(‘\t’) data.append({‘user_id’: str(user), “movie_id”:str(movie_id)}) y.append(float(rating)) users.add(user) items.add(movie_id)

return (data, np.array(y), users, items)

-  **导入训练集和测试集，并转换格式**  
```python
(train_data, y_train, train_users, train_items) = dataLoader("ua.base")
(test_data, y_test, test_users, test_items) = dataLoader("ua.test")
v = DictVectorizer()
X_train = v.fit_transform(train_data)
X_test = v.transform(test_data)

• 训练模型并测试

  # 训练FM
  fm = pylibfm.FM(num_factors=10, num_iter=100, verbose=True, task="regression", initial_learning_rate=0.001, learning_rate_schedule="optimal")
  fm.fit(X_train,y_train)
  

• 预测结果打印误差

  preds = fm.predict(X_test)
  from sklearn.metrics import mean_squared_error
  print("FM MSE: %.4f" % mean_squared_error(y_test,preds))
  # FM MSE: 0.8873
  

3.2.4.2 分类任务实战

• 数据处理
  ```python import numpy as np from sklearn.feature_extraction import DictVectorizer from sklearn.model_selection import train_test_split from pyfm import pylibfm

from sklearn.datasets import make_classification

X, y = make_classification(n_samples=1000,n_features=100, n_clusters_per_class=1) data = [ {v: k for k, v in dict(zip(i, range(len(i)))).items()} for i in X]

X_train, X_test, y_train, y_test = train_test_split(data, y, test_size=0.1, random_state=42)

v = DictVectorizer() X_train = v.fit_transform(X_train) X_test = v.transform(X_test)

-  建立模型并训练  
```python
fm = pylibfm.FM(num_factors=50, num_iter=10, verbose=True, task="classification", initial_learning_rate=0.0001, learning_rate_schedule="optimal")
fm.fit(X_train,y_train)

• 预测结果，由于是分类任务，误差函数肯定不一样

  from sklearn.metrics import log_loss
  print("Validation log loss: %.4f" % log_loss(y_test,fm.predict(X_test)))
  # Validation log loss: 1.3678
  

3.2.5 从零开始实现FM

实现代码如下

import pandas as pd
import numpy as np

from tensorflow.keras import *
from tensorflow.keras.layers import *
from tensorflow.keras.models import *
from tensorflow.keras.callbacks import *
import tensorflow.keras.backend as K

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from tqdm import tqdm


# dense特征取对数　　sparse特征进行类别编码
def process_feat(data, dense_feats, sparse_feats):
    df = data.copy()
    # dense
    df_dense = df[dense_feats].fillna(0.0)
    for f in tqdm(dense_feats):
        df_dense[f] = df_dense[f].apply(lambda x: np.log(1 + x) if x > -1 else -1)

    # sparse
    df_sparse = df[sparse_feats].fillna('-1')
    for f in tqdm(sparse_feats):
        lbe = LabelEncoder()
        df_sparse[f] = lbe.fit_transform(df_sparse[f])

    df_new = pd.concat([df_dense, df_sparse], axis=1)
    return df_new


# FM 特征组合层
class crossLayer(layers.Layer):
    def __init__(self, input_dim, output_dim=10, **kwargs):
        super(crossLayer, self).__init__(**kwargs)

        self.input_dim = input_dim
        self.output_dim = output_dim
        # 定义交叉特征的权重
        self.kernel = self.add_weight(name='kernel',
                                      shape=(self.input_dim, self.output_dim),
                                      initializer='glorot_uniform',
                                      trainable=True)

    def call(self, x):  # 对照上述公式中的二次项优化公式一起理解
        a = K.pow(K.dot(x, self.kernel), 2)
        b = K.dot(K.pow(x, 2), K.pow(self.kernel, 2))
        return 0.5 * K.mean(a - b, 1, keepdims=True)


# 定义FM模型
def FM(feature_dim):
    inputs = Input(shape=(feature_dim,))

    # 一阶特征
    linear = Dense(units=1,
                   kernel_regularizer=regularizers.l2(0.01),
                   bias_regularizer=regularizers.l2(0.01))(inputs)

    # 二阶特征
    cross = crossLayer(feature_dim)(inputs)

    # 将一阶特征与二阶特征相加构建FM模型
    add = Add()([linear, cross])

    pred = Activation('sigmoid')(add)
    model = Model(inputs=inputs, outputs=pred)

    model.summary()
    model.compile(loss='binary_crossentropy',
                  optimizer=optimizers.Adam(),
                  metrics=['binary_accuracy'])

    return model


# 读取数据
print('loading data...')
data = pd.read_csv('./dataset/kaggle_train.csv')

# dense 特征开头是I，sparse特征开头是C，Label是标签
cols = data.columns.values
dense_feats = [f for f in cols if f[0] == 'I']
sparse_feats = [f for f in cols if f[0] == 'C']

# 对dense数据和sparse数据分别处理
print('processing features')
feats = process_feat(data, dense_feats, sparse_feats)

# 划分训练和验证数据
x_trn, x_tst, y_trn, y_tst = train_test_split(feats, data['Label'], test_size=0.2, random_state=2020)

# 定义模型
model = FM(feats.shape[1])

# 训练模型
model.fit(x_trn, y_trn, epochs=10, batch_size=128, validation_data=(x_tst, y_tst))

训练结果如下：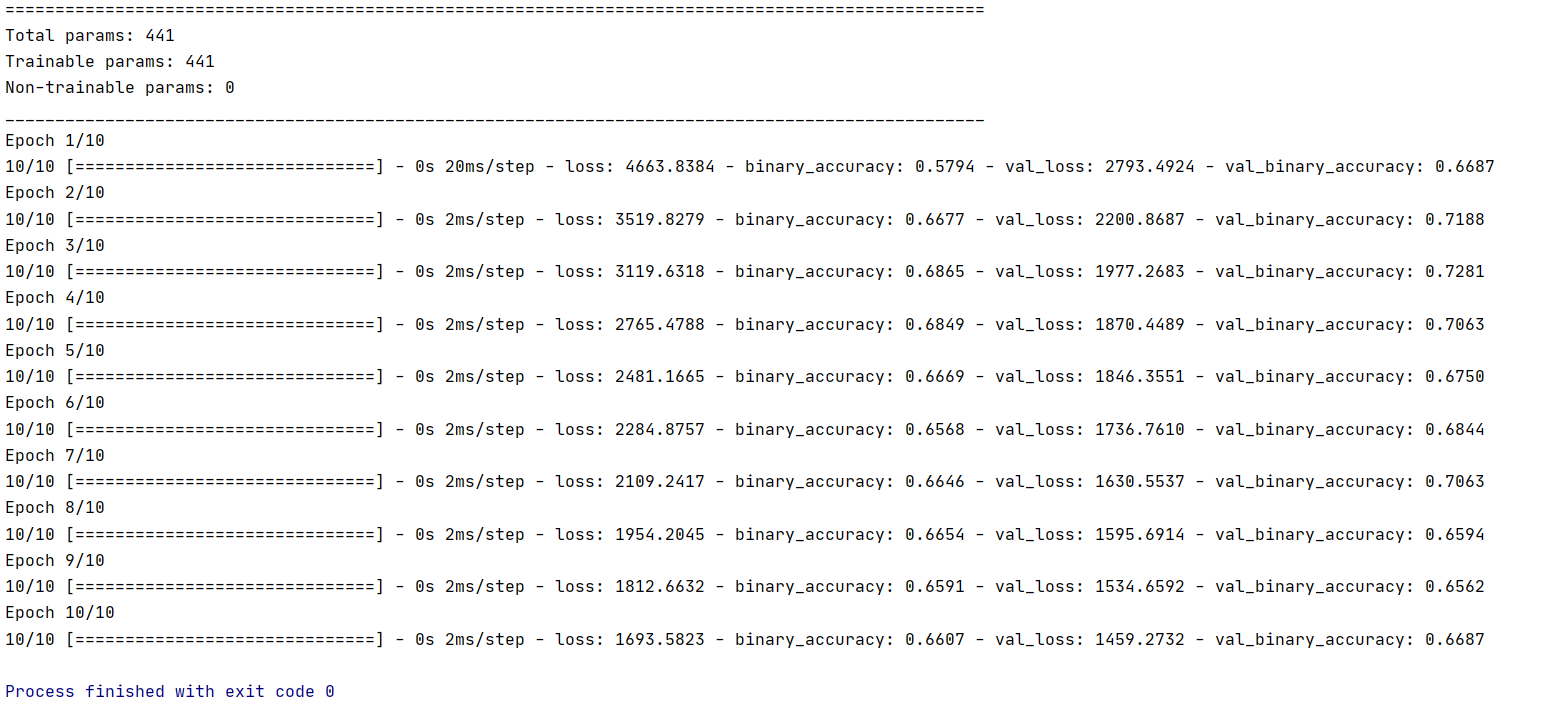

3.3 思考

• 矩阵分解算法后续有哪些改进呢?针对这些改进，是为了解决什么的问题呢？
  这部分可以看看随机奇异值分解（Randomized SVD，RSVD），它的原理如下:
  对于任意矩阵，假定秩为 ，其中，则随机奇异值分解的建模过程可分为三步。
  • 第一步包括三个小步，具体为：
    • 随机生成一个服从高斯分布的矩阵；
    • 计算得到一个大小为的新矩阵
    • 对矩阵 进行QR分解，即。

在该步中，输出的矩阵为 ，其列数为 ，与矩阵是一致的。

• 随机奇异值分解的第二步分为两小步，具体为：
  • 通过与进行矩阵相乘得到一个大小为的新矩阵；
  • ②对矩阵进行奇异值分解，即，其中，矩阵的行数为 ，相比于对矩阵直接进行奇异值分解，这里对相对小一点的矩阵就显得更加“经济”了。

需要注意的是，矩阵的奇异值和右奇异向量同时也是矩阵的奇异值和右奇异向量。

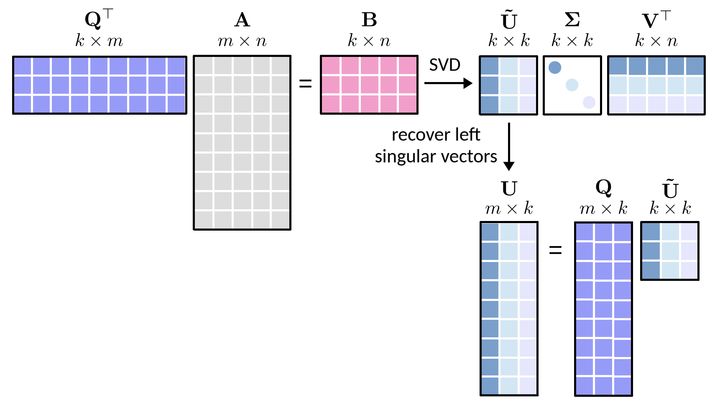
• 随机奇异值分解的第三步是计算矩阵的左奇异向量构成的矩阵，即，其中，是由矩阵的左奇异向量构成的矩阵。

该方法可以有效消除用户和物品打分偏差等。

• 矩阵分解的优缺点分析
  1. 优点：
     • 泛化能力强：一定程度上解决了稀疏问题
     • 空间复杂度低：由于用户和物品都用隐向量的形式存放，少了用户和物品相似度矩阵，空间复杂度由降到了*f#card=math&code=%28n%2Bm%29%2Af&id=ZXoz8)
     • 更好的扩展性和灵活性：矩阵分解的最终产物是用户和物品隐向量，这个深度学习的embedding思想不谋而合，因此矩阵分解的结果非常便于与其他特征进行组合和拼接，并可以与深度学习无缝结合。

1. 缺点：
   • 矩阵分解算法依然是只用到了评分矩阵，没有考虑到用户特征，物品特征和上下文特征，这使得矩阵分解丧失了利用很多有效信息的机会，同时在缺乏用户历史行为的时候，无法进行有效的推荐。

为了解决上述缺点，逻辑回归模型及后续的因子分解机模型，凭借其天然的融合不同特征的能力，逐渐在推荐系统领域得到了更广泛的应用。

• FM存在哪些问题？可以从哪些地方再进行改进？
  FM只能进行线性表达和二阶特征的交互，无法有效处理生活中各种具有复杂结构和规律性的真实数据，因此通过将FM与MLP结合可以有效改进FM的这一缺陷，如之后要介绍的NFM和DeepFM

参考资料

• FunRec：https://gitee.com/giteemirror/fun-rec/
• movielens数据集： https://grouplens.org/datasets/movielens/
• 知乎专栏 RSVD原理：https://zhuanlan.zhihu.com/p/81568119