第三章：栈和队列

3.1 栈

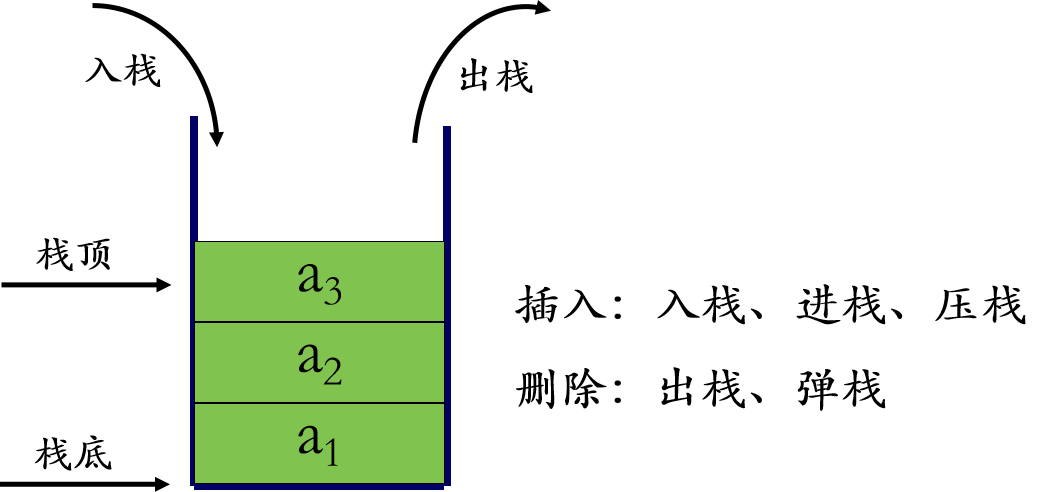
栈的定义

• 限定只能在表的一端进行插入和删除操作的线性表。
• 栈顶(top):允许插入和删除的一端。
• 栈底(bottom):不允许插入和删除的另一端。
• 空栈:不含元素的空表。

eg.( a, a2,……, an)

其中a为栈底元素，an为栈顶元素。

栈的特点

• 先进后出
• 后进先出

栈的抽象数据类型定义

ADT Stack {
    数据对象:D={a,l ai∈ ElemSet, i=1,2.,n, n≥0 }
    数据关系:R1={<a.1,4>l aj-1,4 ∈ D, i=2,..n }
    基本操作:
    InitStack(&S)                   // 操作结果:构造一个空栈S。 
    DestroyStack(&S)                // 初始条件:栈S已存在。 操作结果:栈S被销毁。
    ClearStack(&S)                  // 初始条件:栈S已存在。 操作结果:将S清为空栈
    StackEmpty(S)                   // 初始条件:栈S已存在。 操作结果:若栈S为空栈，则返回TRUE，否则返回FALSE。
    StackLength(S)                  // 初始条件:栈S已存在。 操作结果:返回栈S中元素个数，即栈的长度。
    GetTop(S, &e)                   // 初始条件:栈S已存在且非空。 操作结果:用e返回S的栈顶元素。
    Push(&S, e)                     // 初始条件:栈S已存在。 操作结果:插入元素e为新的栈顶元素。
    Pop(&S, &e)                     // 初始条件:栈S已存在且非空。操作结果:删除S的栈顶元素，并用e 返回其值
    StackTraverse(S, visit( ))      // 初始条件:栈S已存在且非空，visit()为元素的访问函数。操作结果:从栈底到栈顶依次对S的每个元素调用函数
                                        visit()，一旦visit()失败，则操作失败。
}ADT Stack

栈的结构定义

利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。

#define STACK_INIT_SIZE 100;                             //存储空间初始分配量
#define STACKINCREMENT 10;                               //存储空间分配增量
typedef struct {
    SElemType *base;                                     //存储空间基址
    ElemType *top;                                       //栈顶指针
    int stacksize;                                       //当前已分配的存储空间,以元素位单位
}SqStack;

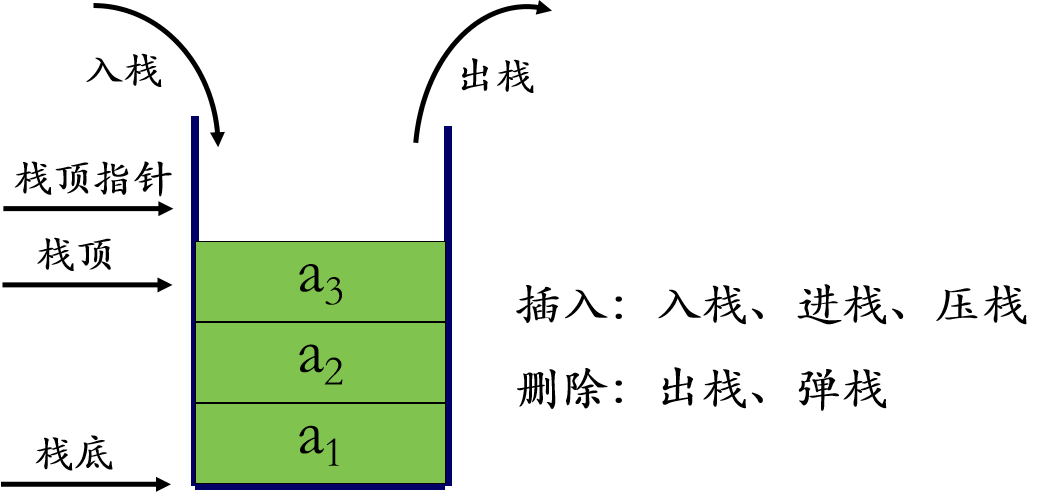
注意：这里的栈顶指针不是栈顶元素，它是指向栈顶元素的下一个存储空间。

栈的基本操作

• 初始化栈

  Status InitStack (SqStack &S){ //构造一个空栈S
    S.base=(SElemType*)malloc(STACK_INIT_SIZE*sizeof(SElemType));//为栈底分配空间    
    if(!S.base) exit(OVERFLOW);          //存储分配失败
    S.top = S.base;                         //空栈的情况就是栈顶指针等于栈底
    S.stacksize = STACK_INIT_SIZE;
    return OK;
  }//InitStack

  所谓初始化就是对栈的结构定义中的所有属性进行赋值。

• 取栈顶元素

  Status GetTop (SqStack S, SElemType &e){    //若栈不空，则用e返回S的栈顶元素，并返回OK
    if (S.top ==S.base ) return ERROR;      //空栈
    e =*(S.top-1);                          //返回非空栈中栈顶元素
    return OK;
  }//GetTop

• 进栈（重点）

  Status Push (SqSttack &S, SElemType{        //插入元素e为新的栈顶元素
    if(S.top.-S.base>=S.stacksize){         //栈满，追加存储空间
        S.base=(SElemType *)realloc(S.base,(S.stacksizetSTACKINC)*sizeof(SElemType));
        if(!S.base) exit(OVERFLOW);             //存储分配失败
        S.top = S.base + S.stacksize;
        S.stacksize += STACKINCREMENT;
    }
    *(S.top++)=e;                           //插入新的元素
    return OK;
  }//Push

• 出栈（重点）

  Status Pop (Stack &S, ElemType &e){    //栈不空，删除S的栈顶元素，用e返回其值，并返回OK;否则返回ERROR
    if (S.top == S.base) return ERROR;   //空栈
    e =*(--S.top);                      //返回非空栈中栈顶元素
    return OK;
  }//Pop

  这里第三句话的意思是：栈顶指针先自减，在把指向的元素赋值给e返回。 上述的操作都是顺序栈（参考顺序表）的操作。

栈的链式存储

入栈算法：
看图了解一下即可，算法很简单可以自己写出来。


出栈算法：

详细的算法在下面的链接中。

数据结构：栈的链式实现（C语言描述）lpp0900320123的专栏-CSDN博客链式栈

顺序栈和链栈的比较

• 时间性能：相同，都是常数时间O(1)。
• 空间性能：
  • 顺序栈：有元素个数的限制和空间浪费的问题。
  • 链栈：没有栈满的问题，只有当内存没有可用空间时才会出现栈满，但是每个元素都需要一个指针域，从而产生了结构性开销（就是所需要的存储空间变大）。

3.2 栈的应用（重点）

数制转换

• 数制转换的规则

十进制数N和其他d进制数的转换：
N= (N div d)×d+ N mod d
计算方法如下：

1. 求出该数对d做整除运算和求余运算的结果。
2. 判断整除运算的结果是不是0，如果不是，把该结果代入第一步中重新计算。
3. 直到整除运算为0，停止运算。
4. 所有求余运算的结果从后往前就是转换进制后的大小。

   (其中: div为整除运算并且取整数，mod为求余运算) eg.十进制和八进制进行转换 N= (N div 8)×8+ N mod 8

举个例子：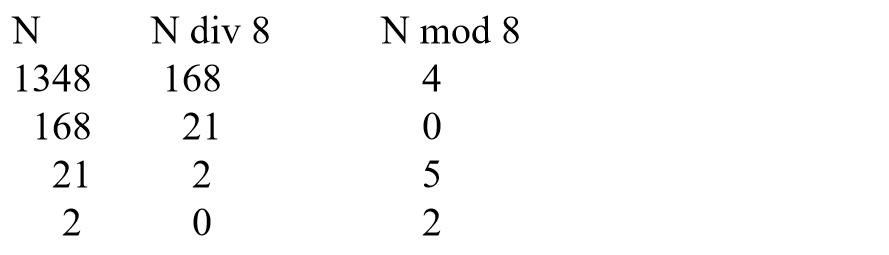

所以十进制数1348转换为八进制为2504。
代入到计算机的算法中，就是每次求出一个求余运算的结果，都把这个结果入栈，以这个上面的题目为例，
入栈的顺序就是4 0 5 2，求完之后出栈的顺序就是2 5 0 4。
核心算法实现：

void conversion (int Num) {   //对于输入的任意一个非负十进制整数，打印输出与其等值的八进制数
    ElemType e; SqStack S;
    InitStack(S);             //构造空栈
    while (Num) {
        Push(S, Num % 8);Num = Num/8;
    }//核心算法，Num不等于0的时候，把余数入栈。
    while (!StackEmpty(S)){
        Pop(S.e);printf ("%d", e);
    }//逐个输出余数。
    printf("\n");
}// conversion

完整代码

#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#include<math.h>
#define STACK_INIT_SIZE 100
#define STACKINCREMENT 10
#define OK 1
typedef int SElemType;
typedef int SElemType;
typedef int Status;
typedef struct {
    SElemType *base;
    SElemType *top;
    int stacksize;
}SqStack;
Status InitStack (SqStack &S){
    S.base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));
    if(!S.base) exit(OVERFLOW);
    S.top= S.base;
    S.stacksize = STACK_INIT_SIZE;
    return OK;
}
Status Push(SqStack &S,SElemType e){
    if(S.top-S.base>=S.stacksize){
        S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
        if(!S.base) exit(-2);
        S.top=S.base+S.stacksize;
        S.stacksize+=STACKINCREMENT;
    }
    *(S.top++)=e;
    return 1;
}
Status StackEmpty(SqStack S){
    if(S.top==S.base) 
        return 1;
    else return 0;
}
Status Pop (SqStack &S,SElemType &e){
    if (S.top == S.base)
        return 0;
    e =*(--S.top);
    return 1;
}
void conversion (int Num){
    SElemType e;
    SqStack S;
    InitStack(S);
    while (Num){
        Push(S, Num % 8);
        Num = Num/8;
    }
    while (!StackEmpty(S)){
        Pop(S,e);
        printf ("%d", e);
    }    
    printf("\n");
}
int main(){
    int a;
    printf("请输入要转换的十进制数：");
    scanf("%d",&a);
    printf("\n转换为八进制的结果为：");
    conversion(a);
    return 0;
}

检测括号匹配

比如说我们要判断下列括号字符串是否符合语法规则。
{}[][(({{}}))]
核心思想就是：

1. 把所有括号字符依次存入栈中。
2. 如果是左括号就直接入栈。
3. 如果是右括号，判断当前的**栈顶元素**是不是相应的右括号。
4. 如果不是，那么该字符串就不符合语法规则。如果是，那么，把当前栈顶元素（也就是这个右括号对应的左括号）出栈。
5. 直到最后一个括号字符出栈/入栈，判断栈中是否还有元素，如果有，那么不符合语法规则；如果没有，符合。

   下面是自制的流程图（我知道非常的搓，凑合看看）

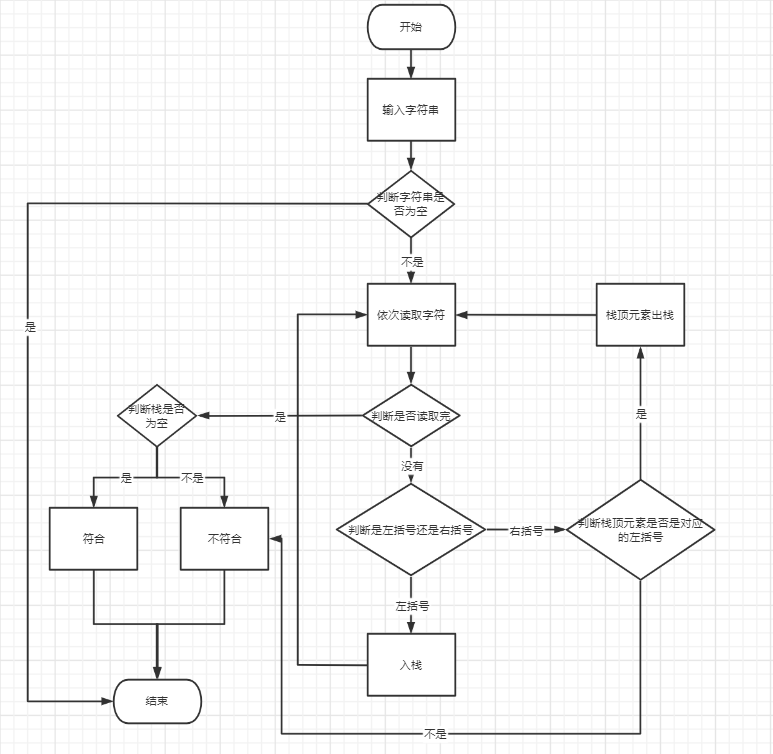
这里就不多bb，直接上完整代码。

/*
    括号匹配检测，对于一串带括号的字符
    1.如果是左括号，入栈
    2.如果是右括号，与栈顶元素比较，
            若形成括号对，则栈顶左括号出栈；
            若不能形成括号对，则括号不能匹配
*/
# include <stdio.h>
# include <stdlib.h>
# define INIT_SIZE 6   //初始栈空间
# define INCRE_SIZE 2  //占空间增量
//栈结构
typedef struct
{
    char * base;  //指向栈空间基址
    char * top;  //指向栈顶元素的下一个位置
    int initsize;  //栈空间大小
}Stack;
Stack inital();  //初始化栈
void push(Stack &s, char ch);  //元素入栈
void pop(Stack &s, char &e);  //元素出栈
bool stack_empty(Stack s);  //判断栈是否为空
int main(void)
{
    Stack s = inital();
    char ch[20];
    char * p;
    char e;
    printf("请输入带括号的字符串:");
    gets(ch);    //输入字符
    p = ch;   //指向首字符
    while(*p)  //没有到串尾
    {
        switch(*p)
        {
            case '(':       
            case '[':
            case '{':
                push(s, *p); //左括号入栈
                p ++;      //读下一个字符
                break;
            case ')':
            case ']':
            case '}':
                pop(s, e);  //读入右括号，与栈顶的左括号e匹配
                if( !((e == '(' && *p == ')') || (e == '['  && *p == ']') || (e == '{' && *p == '}')))
                {
                    printf("左右括号不能匹配\n");
                    exit(0);
                }
                p ++;
                break;
            default:
                p ++;
        }
    }
    if(stack_empty(s))  //栈是否为空，为空，则匹配成功
    {
        printf("括号匹配成功\n");
    }
    else
    {
        printf("括号匹配失败\n");
    }
    return 0;
}
//初始化栈
Stack inital()
{
    Stack s;
    s.base = (char *)malloc(sizeof(char) * INIT_SIZE);
    s.initsize = INIT_SIZE;
    s.top = s.base;
    return s;
}
//入栈
void push(Stack &s, char ch)
{
    if(s.top - s.base >= s.initsize) //栈满，增加栈空间
    {
        s.base = (char *)realloc(s.base, sizeof(char) * (s.initsize + INCRE_SIZE));
        s.initsize = s.initsize + INCRE_SIZE;
    }
    *(s.top) = ch;
    s.top ++;
}
//出栈
void pop(Stack &s, char &e)
{
    if(stack_empty(s))
        return;
    else
    {
        e = *(s.top - 1);
        s.top --;
    }
}
//判断栈是否为空
bool stack_empty(Stack s)
{
    if(s.base == s.top)
        return true;
    else
        return false;
}
————————————————
版权声明：本文为CSDN博主「wjb214149306」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/wjb214149306/article/details/47299749

下面是b站视频讲解。

点击查看【bilibili】

表达式求值

• 表达式的组成
  1. 操作数(operand):常数、变量。
  2. 运算符(operator):算术运算符、关系运算符和逻辑运算符。
  3. 界限符(delimiter):左右括弧和表达式结束符。
• 算术运算的规则
  1. 先乘除后加减先左后右
  2. 先括弧内后括弧外
     例如:
     4+2*3-10/5
     =4+6-10/5
     =10-10/5
     =10-2

     这个好难的我也不会，所以直接上链接。(我估计也不大会考)

点击查看【bilibili】

3.3 队列

队列的基础定义

队列
只允许在一端进行插入而在另一端进行删除的线性表。
队尾：允许插入的一端。
队头：允许删除的一端。
特点：先进先出（FIFO）。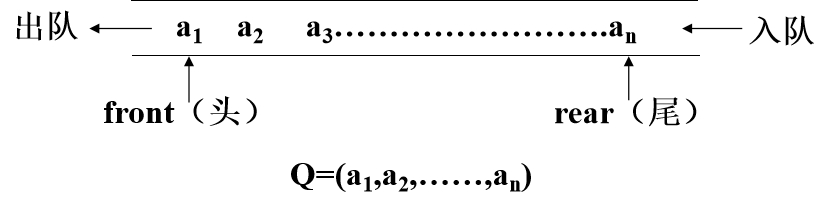

队列的抽象数据类型定义(了解即可）

ADT Queue {
    数据对象:D={ai|ai∈ElemSet, i=1,2....,n, n≥0}
    数据关系:R1={<ai-1,ai>│ ai-1,ai∈D,i=2,....n}
    基本操作:
        InitQueue(&Q)                   //操作结果:构造一个空队列Q。
        DestroyQueue(&Q)                //初始条件:队列Q已存在。操作结果:队列Q被销毁，不再存在。
        ClearQueue(&Q)                  //初始条件:队列Q已存在。操作结果:将Q清为空队列。
        QueueEmpty(Q)                   //初始条件:队列Q已存在。操作结果:若Q为空队列，则返回TRUE,否则返回FAISE。
        QueueLength(Q)                  //初始条件:队列Q已存在。操作结果:返回Q的元素个数，即队列的长度。
        GetHlead(Q,&e)                  //初始条件:Q为非空队列。操作结果:用e 返回Q的队头元素。
        EnQueue(&cQ,e)                  //初始条件:队列Q已存在。操作结果:插入元素e为Q的新的队尾元素。
        DeQueue(&Q,&e)                  //初始条件:Q为非空队列。操作结果:删除Q的队头元素，并用e返回其值。
        QueueT'raverse(Q,visit())       //初始条件:队列Q已存在且非空，visit()为元素的访问函数。操作结果:依次对Q的每个元素调用函数visit( ),
                                          一旦visit(）失败则操作失败。
} ADT Queue

队列的结点定义（重点）

typedef struct QNode{
    Qelemlype data ;
    struct QNode *next ;
}QNode, *QueuePtr;
typedef struct{
    QueuePtr front ;//队头指针
    QueuePtr rear ;//队尾指针
}LinkQueue;

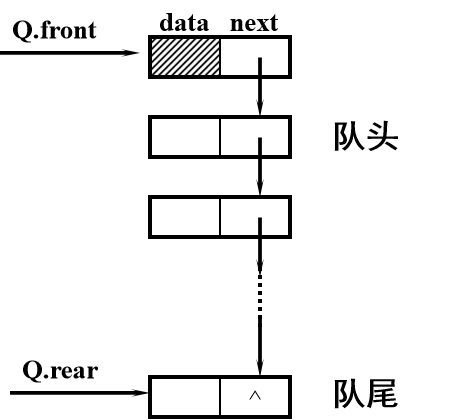
这里的第一个Q.front指向是一个空指针，所以队头是next指向的结点。

不难看出，队列是基于链表的发展。

基本操作

• 创造一个空队列Q

  Status InitQueue (LinkQueue &Q){//构造一个空队列Q
    Q.front=Q.rear=(QueuePtr)malloc(sizeof(QNode));
    if (!Q.front) exit(OVERFOLW);/存储分配失败
    Q.front->next=NULL;
    return OK;
  }

  首先使队列的头指针和尾指针指向同一个存储空间。 判断是否还存在存储空间，若不存在，则创建空列队Q失败。 令头指针的下一个指针为空指针。

• 入队列

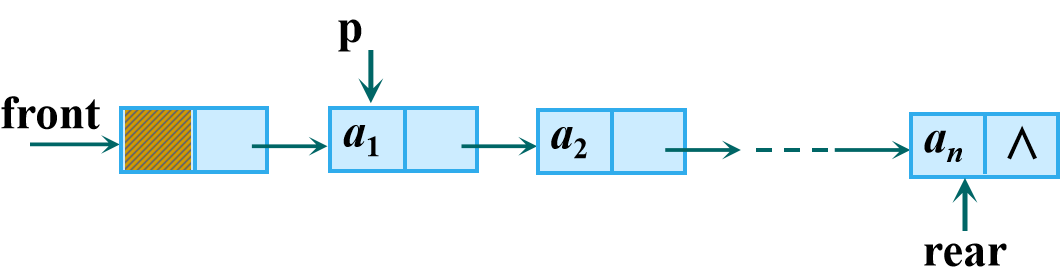
  Status EnQueue(LinkQueue &Q,QElemType e){
    //在当前队列的尾元素之后，插入元素e为新的队列尾元素
    p=(QueuePtr)malloc(sizeof(QNode));
    if (!p) exit(OVERFLOW);            //存储分配失败
    p->data=e;p->next = NULL;
    Q.rear->next=p;                    //修改尾结点的指针
    Q.rear=p;                        //移动队尾指针
  }

  如下图所示
  
  
  

• 出队列

  Status DeQueue(LinkQueue &Q,QElem.Type &e){
    //若队列不空，则删除队列Q的队头元素，用e返回其值，并返回OK;
    //否则返回ERROR
    if(Q.front==Q.rean) return ERROR;    //链队列空
    p=Q.front->next;
    e= p->data;                            //返回被删元素的值
    Q.front->next=p->next;                //修改队头结点指针
    if(Q.rear == p) Q.rear=Q.front;
    free(p);
    //释放被删结点
    return OK;
  }

  过程如下图所示
  
  

队列存在的问题

问题：假溢出
什么是假溢出，我们举个例子，假设一个队列的存储空间为6。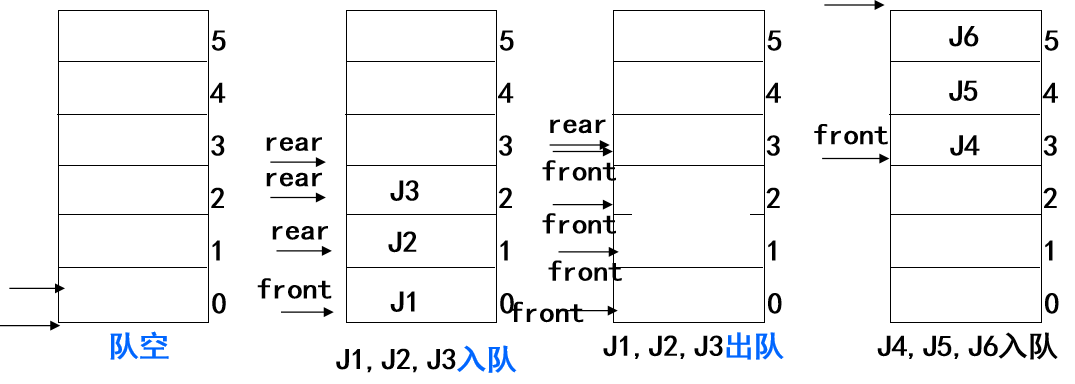

经过上述入队和出队操作后，rear指针不断被提高，会导致后面J4，J5，J6入队之后，不能再入队J7（已经栈满了），然而实际情况是队列仍然存在存储空间。
所以下面引入了循环队列。

循环队列

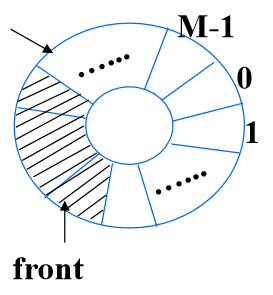
• 基本思想：把队列设想成环形，让sq[0]接在sq[M-1]之后，若rear+1==M,则令rear=0;
• 入队： sq[rear]=x; rear=(rear+1)%M;
• 出队： x=sq[front]; front=(front+1)%M;

• 结构定义

  循环队列的结构定义
  #define MAXQSIZE 100//最大队列长度
  typedef struct {
    QElemType *base //初始化的动态分配存储空间
    int rear        //队尾指针，指向队尾元素
    int front        //队头指针，指向队头元素的前一个位置
  }SqQueue

• 创建一个空队列

  Status InitQueue (SqQueue &Q){//构造一个空队列Q
    Q.base = (QElemType *)malloc(MAXQSIZE*sizeof(QElemType));//为循环队列分配存储空间
    if (!Q.base) exit(OVERFLOW);                             //存储分配失败
    Q.front = Q.rear= 0;
    return OK;
  }// InitQueue

• 求队列的长度

  int QueueLength (SqQueue Q){
  //返回队列Q中元素个数，即队列的长度
    return ((Q.rear-Q.fron+MAXQSIZE)%MAXQSIZE);
  }

• 入队操作

  Status EnQueue (SqQueue &Q,QElemType e){
    //插入元素e为新的队列尾元素
    if((Q.rear+1)%MAXQSIZE==Q.front ) return ERROR; //队列满
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear+1) % MAXQSIZE;
    return OK;
  }

• 出队操作

  Status DeQueue (SqQueue &Q,QElemType &e){
    //若队列不空，则删除当前队列Q中的头元素，用e返回其值,并返回OK
    if (Q.front== Q.rear) return ERROR;
    e = Q.base[Q.front];
    Q.front =(Q.front+1) % MAXQSIZE;
    return OK;
  }